Minimaler Spannbaum: Unterschied zwischen den Versionen

Aus SibiWiki
Zur Navigation springen Zur Suche springen
 
(3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt)
Zeile 1: Zeile 1:
[[Kategorie:Informatik]]
[[Kategorie:Informatik]]
[[Kategorie:Informatik-Abitur]]
[[Kategorie:Informatik-Q1]]
[[Kategorie:Datenstrukturen(IF)]]
[[Kategorie:Datenstrukturen(IF)]]


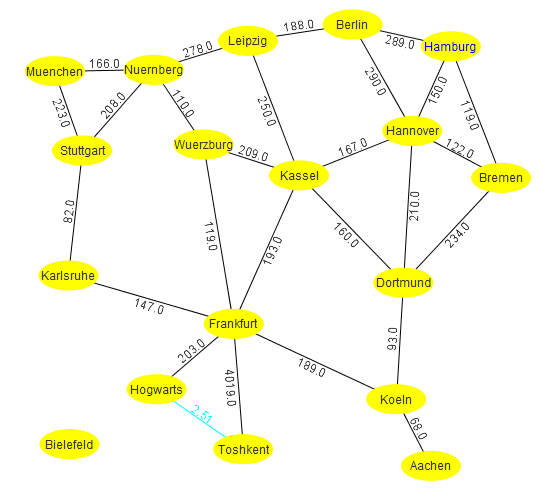
[[File:Landkarte-original.png|thumb|Original-Landkarte |400px]]
[[File:Landkarte-original.png|thumb|Original-Landkarte |400px]]


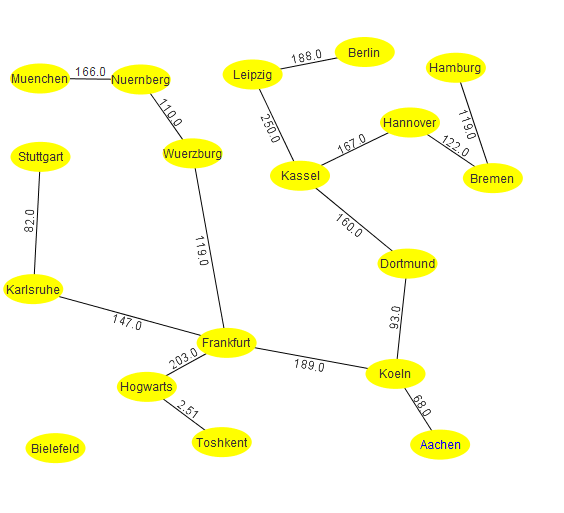
[[File:Landkarte-minimaler-spannbaum.png|thumb|Minimaler Spannbaum |400px]]
[[File:Landkarte-minimaler-spannbaum.png|thumb|Minimaler Spannbaum |400px]]
Minimale Spannbäume beziehen sich auf [[Graph|Graphen]].
''Sie sind '''nur für den LK''' relevant!


=Definition=
=Definition=
Zeile 14: Zeile 19:
==Beispiel aus der Praxis==
==Beispiel aus der Praxis==
Eine Stromfirma will ein Leitungsnetz aufbauen, das alle Städte verbindet. Keine Stadt darf ausgelassen werden. Das Stromnetz soll aber möglichst kurz sein.
Eine Stromfirma will ein Leitungsnetz aufbauen, das alle Städte verbindet. Keine Stadt darf ausgelassen werden. Das Stromnetz soll aber möglichst kurz sein.
=Implementierung=
#Zu Anfang erzeugt man einen <code>ergebnisgraph</code>, der nur die Knoten des ursprünglichen Graphen enthält, aber nicht die Kanten.
#Alle Kanten des gesamten ursprünglichen Graphen werden ausgelesen werden ihrem Gewicht nach durchgegangen, wobei man beim kleinsten Gewicht anfängt.
##Kann die momentan betrachtete Kante in den <code>ergebnisgraph</code> eingefuegt werden, ohne dass ein Kreis entsteht, wird sie eingefügt.
'''Hauptmethode'''
<code>
  public Graph minimalerSpannbaum(Graph pGraph){
    //es wird ein neuer Graph erstellt, der das Ergebnis hinterher anzeigt
    Graph ergebnisGraph = new Graph();
    //alle Knoten des uebergebenen Graphen werden
    //in den spaeteren Ergebnisgraphen eingetragen
    List nodes = pGraph.getNodes();
    nodes.toFirst();
    while(nodes.hasAccess()){
        GraphNode akt = (GraphNode)nodes.getObject();
        ergebnis.addNode(akt);
        nodes.next();
    }
    List edges = alleEdgesSortiert(pGraph);
    //diese Liste wird duchgegangen
    for(edges.toFirst(); edges.hasAccess(); edges.next()){
    //kann die aktuell in der Liste betrachtete Kante eingefuegt werden,
    //ohne dass ein Kreis entsteht, wird sie eingefuegt   
    Edge akt = (Edge)edges.getObject();
        if(!erzeugtKreis(ergebnisGraph, edges.elementAt(i))){
          ergebnisGraph.addEdge(akt.getNodeA(), akt.getNodeB(), akt.getWeight());
          System.out.println("addEdge: "+akt);
        }
    }
    return ergebnisGraph;
  }
</code>
'''Hilfsmethoden'''
Für die Überpruefung ob ein Kreis erzeugt wird ist eine eigene Methode hilfreich.
Hier wird von einem Knoten der einzufuegenden Kantre ausgehend ueberprueft, ob der andere Knoten erreichbar ist.
Wenn ja, dann würde durch Einfügen ein Kreis erzeugt, wenn nein nicht.
<code>
  private boolean erzeugtKreis(Graph pGraph, Edge pEdge) {
    //von dem einen Knoten aus erreichbare Nodes
    //werden ausgelesen un in einer Liste gespeichert...
    List erreichbare = erreichbareNodes(pGraph, pEdge.getNodeA());
    //...und werden durchlaufen
    erreichbare.toFirst();
    while(erreichbare.hasAccess()){
        //wird der Knoten, von dem ausgegangen wurde, gefunden,
        //wurde ein Kreis erzeugt und true ausgegeben
        if(pEdge.getNodeB() == (GraphNode)erreichbare.getObject()){
          return true;
        }
        erreichbare.next();
    }
    //wird der Knoten nicht gefunden, wird false zurueckgegeben,
    //da kein Kreis erzeugt wuerde
    return false;
  }
</code>

Aktuelle Version vom 11. November 2015, 09:24 Uhr


Original-Landkarte
Minimaler Spannbaum

Minimale Spannbäume beziehen sich auf Graphen.

Sie sind nur für den LK relevant!

Definition

Ein Minimaler Spannbaum besteht aus einer Liste von Kanten des Graphen, die folgenden Bedingungen genügen muss:

  1. die Kanten der Liste müssen alle Knoten des Graphen miteinander verbinden.
  2. die Gesamtlänge der Kanten in der Liste muss (im Hinblick auf die Erfüllung der 1. Bedingung) minimal sein.

Beispiel aus der Praxis

Eine Stromfirma will ein Leitungsnetz aufbauen, das alle Städte verbindet. Keine Stadt darf ausgelassen werden. Das Stromnetz soll aber möglichst kurz sein.

Abgerufen von „https://sibiwiki.de/wiki/index.php?title=Minimaler_Spannbaum&oldid=2060“