Binärbaum (Methoden)

Diese Seite entspricht dem Abi 17 (und folgenden)

Hier werden die Standard-Strategien für das Durchlaufen von Binärbäumen vorgestellt:

• Rekursion
• Durchlaufen eines Pfades mit einer while-Schleife
• Linearisierung

Außerdem wird erklärt, was eine Rahmenmethode ist und wie man sie implementiert.

Für das Suchen und Löschen von Elementen: siehe binärer Suchbaum ab Abi 2017

Fachbegriffe

Rekursion, Abbruchbedingung, rekursiver Aufruf, Sachlogik, Rahmenmethode, Pfaddurchlauf, Linearisierung, Baumliste

Standard-Strategien

Für das Durchlaufen von Binärbäumen gibt es drei Standard-Strategien:

• Rekursion
• Durchlaufen eines Pfades mit einer while-Schleife
• Linearisierung

Rekursion

Binärbäume sind rekursive Datenstrukturen, denn jeder Binärbaum hat zwei Teilbäume - und die sind selber wieder Binärbäume.

Deswegen bietet es sich an, Binärbäume rekursiv zu durchlaufen.

Strategie

Bei der Implementierung einer rekursiven Methode für Binärbäume wird der gesamte Baum nur sehr grob betrachtet: Er besteht aus

• der Wurzel,
• dem linken Teilbaum (für den die Methode rekursiv aufgerufen wird)
• dem rechten Teilbaum (für den die Methode nochmal rekursiv aufgerufen wird).

In der Sachlogik muss man folgende Frage beantworten:

Wie setzt sich das Gesamtergebnis aus der Wurzel, dem Ergebnis des linken Teilbaumes und dem Ergebnis des rechten Teilbaumes zusammen? Erklärvideo zur rekursiven Strategie

Bestandteile einer rekursiven Methode:

• eine Abbruchbedingung oder mehrere Abbruchbedingungen.
  Diese hängen vom Sachzusammenhang ab - in der Regel braucht man mindestens eine Abbruchbedingung für einen leeren Binärbaum.
• Wurzel auslesen (=Wurzelbehandlung)
• rekursive Aufrufe: Die Methode ruft sich selber auf.
  • Meistens braucht man zwei rekursive Aufrufe: einen für den linken Teilbaum und einen für den rechten Teilbaum.
  • Bei Methoden, die etwas zurückgeben, muss man sich für den Rückgabewert interessieren!
• Sachlogik: Hier werden die Wurzel und die Ergebnisse der rekursiven Aufrufe behandelt.

Implementierung

Das rekursive Vorgehen wird hier beispielhaft an der Methode public int summe(BinaryTree<Integer> pTree) aufgezeigt:

   public int summe(BinaryTree<Integer> pTree){
       int ergebnis = 0;
 
       //Abbruchbedingung
       if(pTree.isEmpty()){
           return ergebnis;
       }
 
       //Wurzel auslesen
       int wurzel = pTree.getContent();
  
       //rekursive Aufrufe
       int summeLinks =  summe(pTree.getLeftTree());
       int summeRechts = summe(pTree.getRightTree());
 
       //Sachlogik
       ergebnis += wurzel;
       ergebnis += summeLinks;
       ergebnis += summeRechts;

       return ergebnis;
   }

Durchlaufen eines Pfades

In manchen Situationen, vor allem in Bäumen mit Suchbaumstruktur, reicht es, wenn man einen Pfad von der Wurzel bis zu einem Blatt durchläuft. Das lässt sich mit einer while-Schleife realisieren, d.h. Rekursion ist hier nicht nötig.

Strategie

Um einen Pfad in dem Binärbaum pTree von der Wurzel zu einem Blatt zu durchlaufen, geht man wie folgt vor:

• Es wird eine while-Schleife geöffnet, die so lange läuft, bis pTree leer ist.
• In der while-Schleife wird - abhängig von der Sachlogik - nach links oder nach rechts abgebogen. Das realisiert man, indem man pTree durch seinen linken oder rechten Teilbaum updated.
• Nach Beendigung der while-Schleife ist man dann bei einem leeren Knoten unterhalb eines Blattes angekommen.

Implementierung

Als Beispiel wird die Methode einfuegen für einen mit Zahlen gefüllten Suchbaum implementiert.

   public void einfuegen(BinaryTree<Integer> pTree, int pZahl) {
      //Hilfsbaum definieren, damit man pTree nicht "zersägt":
      BinaryTree<Integer> b = pTree;
      while(!b.isEmpty()){
           int wurzel = b.getContent();
           // UPDATE von pTree
           if(pZahl < wurzel){
               b = b.getLeftTree();
           }
           else{
               b = b.getRightTree();
           }
       }
       // jetzt ist man beim richtigen leeren Knoten angekommen!
       b.setContent(pZahl);
   }

Linearisierung

Linearisierung ist eine Strategie, wie man rekursive Strukturen (z.B. einen Binärbaum) komplett durchlaufen kann, OHNE eine rekursive Methode zu verwenden.

Vorgehensweise

Die Vorgehensweise wird hier am Beispiel Levelorder aufgezeigt. In Levelorder wird der Binärbaum "schichtenweise" von oben nach unten durchlaufen, d.h. es handelt sich hier um eine Breitensuche.

Die Idee der Linarisierung ist die folgende:

Linearisierung:

1. eine Hilfsliste baumListe wird angelegt; in diese Hilfsliste kommen nur Bäume!
2. der ganze Baum wird in baumListe gepackt, d.h. baumListe hat jetzt ein Element.
3. dann wird baumListe mit einer Schleife von vorne bis zum Ende durchlaufen; dabei wird baumListe ständig ergänzt!
   1. bei jedem Schleifen-Durchlauf wird das aktuelle Element (=ein Baum) aus baumListe entnommen.
   2. die beiden Teilbäume (wenn sie nicht leer sind) werden hinten an baumListe angehängt.
4. Jetzt hat man in baumListe eine Liste aller Teilbäume von pTree.
   1. Diese Liste kann jetzt für die Sachlogik verwendet werden.

Sachlogik:

1. eine Ergebnisliste ergebnisListe wird angelegt; in ergebnisListe kommen die Knoten in der Levelorder-Reihenfolge.
2. baumListe wird mit einer Schleife durchlaufen. Bei jedem Schleifendurchlauf wird...
   1. der aktuelle Baum aus baumListe ausgelesen.
   2. die Wurzel des aktuellen Baumes in ergebnisListe eingefügt.

Implementierung

   public List<Object> levelorder(BinaryTree<Object> pTree){
       //Linearisierung
       List<BinaryTree<Object>> baumListe = new List<>();
       baumListe.append(pTree);
       baumListe.toFirst();
       while(baumListe.hasAccess()){
           BinaryTree<Object> aktuell = baumListe.getContent();
           if(!aktuell.getLeftTree().isEmpty()){
               baumListe.append(aktuell.getLeftTree());
           }
           if(!aktuell.getRightTree().isEmpty()){
               baumListe.append(aktuell.getRightTree());
           }
           baumListe.next();
       }
       // Sachlogik:
       // die baumListe durchlaufen,
       // von jedem Element (Typ: BinaryTree!)
       // die Wurzel auslesen und an ergebnisListe anhaengen
       List<Object> ergebnisListe = new List<>();
       baumListe.toFirst();
       while(baumListe.hasAccess()){
           BinaryTree<Object> aktuellerBaum = baumListe.getContent();
           Object aktuelleWurzel = aktuellerBaum.getContent();
           ergebnisListe.append(aktuelleWurzel);
           baumListe.next();
       }
       return ergebnisListe;
   }

Rahmenmethode

siehe Rahmenmethode im Artikel Binärbaum.

weitere beispielhafte Methoden

Tiefe

public int tiefe(BinaryTree<Object> pTree) {
   int ergebnis = -1;
   if (pTree.isEmpty()) {
      // leere Teilbaeume haben Tiefe -1
      // denn Baeume, die nur aus einem Blatt bestehen, 
      // haben Tiefe 0!
      return ergebnis;
   }
   // die Wurzel beruecksichtigen!
   // Bäume mit nur einer Wurzel haben die Tiefe 0.
   ergebnis = 0;
   int tiefeLinks = tiefe(pTree.getLeftTree());
   int tiefeRechts = tiefe(pTree.getRightTree());
   ergebnis = tiefeLinks;
   if (ergebnis < tiefeRechts) {
      ergebnis = tiefeRechts;
   }
   return ergebnis;
}

Knotenzahl

public int knotenzahl(BinaryTree<Object> pTree) {
   int ergebnis = 0;
   if (pTree.isEmpty()) {
      return ergebnis;
   }
   ergebnis += 1;   // die Wurzel zaehlen!
   int knotenLinks = knotenzahl(pTree.getLeftTree());
   int knotenRechts = knotenzahl(pTree.getRightTree());
   ergebnis += knotenLinks;
   ergebnis += knotenRechts;
   return ergebnis;
}

Blätter

Diese Methode gibt alle Blätter eines Baumes in einer Liste zurück.

Die Methode funktioniert rekursiv.

Man braucht zwei Abbruchbedingungen:

• für einen leeren Baum -> eine leere Liste zurückgeben
• für ein Blatt -> eine Liste mit nur einem Blatt drin zurückgeben

public List blaetter(BinaryTree<Object> pTree) {
   List ergebnis = new List();

   if (pTree.isEmpty()) {
      return ergebnis;
   }

   if (pTree.getLeftTree().isEmpty() && pTree.getRightTree().isEmpty()){
      // pTree ist ein Blatt!
      ergebnis.append(pTree);
      return ergebnis;
   }

   List<Object> linkesErgebnis = blaetter(pTree.getLeftTree());
   List<Object> rechtesErgebnis = blaetter(pTree.getRightTree());

   ergebnis.concat(linkesErgebnis);
   ergebnis.concat(rechtesErgebnis);

   return ergebnis;
}

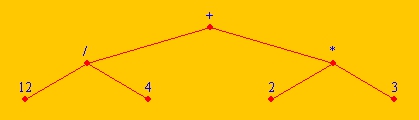
Berechnen

Binärer Strukturbaum (12/4)+(2*3)

Diese Methode berechnet das Ergebnis eines Strukturbaumes aus den Rechenzeichen +, -, *, / und Zahlen.

public double berechnen(BinaryTree<String> b) {
   double ergebnis = 0;
   if (b.isEmpty()) {
      return ergebnis;
   }
   String wurzelString = b.getContent();
   if ( !wurzelString.equals("+") &&
        !wurzelString.equals("-") &&
        !wurzelString.equals("*") &&
        !wurzelString.equals("/") 
      ) 
   {
       double wurzelDouble = Double.parseDouble(wurzelString);
       ergebnis = wurzelDouble;
       return ergebnis;
   }

   double ergebnisLinks  = berechnen(b.getLeftTree());
   double ergebnisRechts = berechnen(b.getRightTree());

   if(wurzelString.equals("+")){
       ergebnis = ergebnisLinks + ergebnisRechts;
   }
   else if((wurzelString.equals("-")){
       ergebnis = ergebnisLinks - ergebnisRechts;
   }
   else if((wurzelString.equals("*")){
       ergebnis = ergebnisLinks * ergebnisRechts;
   }
   else if((wurzelString.equals("/")){
       ergebnis = ergebnisLinks / ergebnisRechts;
   }
   else{
       System.err.println("unbekanntes Rechenzeichen!");
       ergebnis = 0;
   }
   return ergebnis;
}