Quicksort: Unterschied zwischen den Versionen
K (Akaibel verschob Seite Quicksort ab Abi 2017 nach Quicksort) |
|||
| (5 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 9: | Zeile 9: | ||
<font color='red'>'''Diese Seite entspricht dem Abi 17 (und folgenden)'''</font> | <font color='red'>'''Diese Seite entspricht dem Abi 17 (und folgenden)'''</font> | ||
=Fachbegriffe= | |||
rekursiv, Divide-Conquer-Prinzip, Pivot-Element, Abbruchbedingung, Laufzeit | |||
=Prinzip= | =Prinzip= | ||
Quicksort arbeitet nach dem '''Divide-and-Conquer-Prinzip''': | Quicksort arbeitet nach dem '''Divide-and-Conquer-Prinzip''': | ||
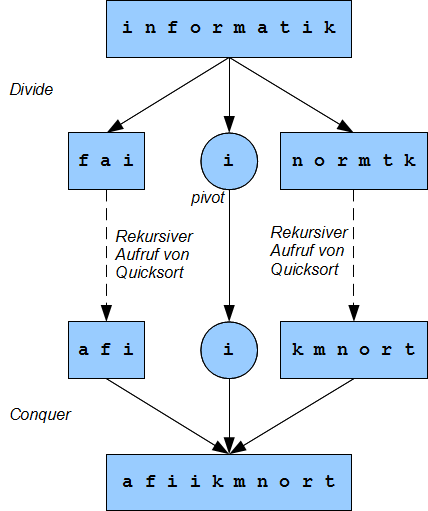
Zunächst wird die zu sortierende Liste in zwei Teillisten („linke“ und „rechte“ Teilliste) getrennt (='''Divide'''). Dazu wählt Quicksort ein sogenanntes '''Pivotelement''' aus der Liste aus. Alle Elemente, die kleiner als das Pivotelement sind, kommen in die linke Teilliste, und alle, die größer sind, in die rechte Teilliste. Die Elemente, die gleich dem Pivotelement sind, können sich beliebig auf die Teillisten verteilen. Nach der Aufteilung sind die Elemente der linken Liste kleiner oder gleich den Elementen der rechten Liste. | Zunächst wird die zu sortierende Liste in zwei Teillisten („linke“ und „rechte“ Teilliste) getrennt (='''Divide'''). Dazu wählt Quicksort ein sogenanntes '''Pivotelement''' aus der Liste aus. Alle Elemente, die kleiner als das Pivotelement sind, kommen in die linke Teilliste, und alle, die größer sind, in die rechte Teilliste. Die Elemente, die gleich dem Pivotelement sind, können sich beliebig auf die Teillisten verteilen. Nach der Aufteilung sind die Elemente der linken Liste kleiner oder gleich den Elementen der rechten Liste. | ||
Anschließend wird jede Teilliste in sich sortiert | Anschließend wird jede Teilliste in sich sortiert, indem der Quicksort-Algorithmus '''rekursiv''' auf die linke und die rechte Teilliste angewendet werden. Wenn eine Teilliste nur ein oder kein Element enthält, bricht die Rekursion ab, d. h. für diese Teilliste wird Quicksort nicht mehr aufgerufen. | ||
Am Ende werden die beiden Teillisten und das Pivot-Element zusammengeführt (='''Conquer'''). | Am Ende werden die beiden Teillisten und das Pivot-Element zusammengeführt (='''Conquer'''). | ||
| Zeile 34: | Zeile 39: | ||
<code> | <code> | ||
public List<Person> quicksort(List<Person> pList){ | |||
'''// leere Ergebnis-Liste erzeugen''' | |||
List<Person> ergebnis = new ListWithViewer<Person>(); | |||
'''// Abbruchbedingung für die leere Liste''' | |||
if(pList.isEmpty()){ | |||
return ergebnis; | |||
} | |||
'''// das erste Element der Liste als Pivot-Element festlegen''' | |||
pList.toFirst(); | |||
Person pivot = pList.getContent(); | |||
'''// zum nächsten Element gehen''' | |||
pList.next(); | |||
'''// die Listen links und rechts als leere Listen erzeugen | |||
List<Person> links = new List<Person>(); | |||
List<Person> rechts = new List<Person>(); | |||
'''// pList durchlaufen und die Elemente mit pivot vergleichen:''' | |||
'''// kleinere kommen nach links, die anderen nach rechts.''' | |||
while(pList.hasAccess()){ | |||
Person p = pList.getContent(); | |||
if(p.getEinkommen() < pivot.getEinkommen()){ | |||
links.append(p); | |||
} | |||
else{ | |||
rechts.append(p); | |||
} | |||
pList.next(); | |||
} | |||
'''// rekursive Aufrufe von quicksort für links und rechts''' | |||
List<Person> linksSortiert = quicksort(links); | |||
List<Person> rechtsSortiert = quicksort(rechts); | |||
'''// die sortierten Teillisten und das Pivot-Element''' | |||
'''// in der richtigen Reihenfolge an ergebnis anhängen''' | |||
ergebnis.concat(linksSortiert); | |||
ergebnis.append(pivot); | |||
ergebnis.concat(rechtsSortiert); | |||
'''// die ergebnis-Liste zurückgeben''' | |||
return ergebnis; | |||
} | |||
</code> | |||
</code> | |||
Aktuelle Version vom 23. Januar 2022, 16:52 Uhr
im Zentralabitur nur relevant für den LK!
Diese Seite entspricht dem Abi 17 (und folgenden)
Fachbegriffe
rekursiv, Divide-Conquer-Prinzip, Pivot-Element, Abbruchbedingung, Laufzeit
Prinzip
Quicksort arbeitet nach dem Divide-and-Conquer-Prinzip:
Zunächst wird die zu sortierende Liste in zwei Teillisten („linke“ und „rechte“ Teilliste) getrennt (=Divide). Dazu wählt Quicksort ein sogenanntes Pivotelement aus der Liste aus. Alle Elemente, die kleiner als das Pivotelement sind, kommen in die linke Teilliste, und alle, die größer sind, in die rechte Teilliste. Die Elemente, die gleich dem Pivotelement sind, können sich beliebig auf die Teillisten verteilen. Nach der Aufteilung sind die Elemente der linken Liste kleiner oder gleich den Elementen der rechten Liste.
Anschließend wird jede Teilliste in sich sortiert, indem der Quicksort-Algorithmus rekursiv auf die linke und die rechte Teilliste angewendet werden. Wenn eine Teilliste nur ein oder kein Element enthält, bricht die Rekursion ab, d. h. für diese Teilliste wird Quicksort nicht mehr aufgerufen.
Am Ende werden die beiden Teillisten und das Pivot-Element zusammengeführt (=Conquer).
Laufzeit
Quicksort hat im Average Case die Laufzeit O(n*log(n)).
Im Worst Case steigt die Laufzeit auf O(n2).
Da der Worst Case nur für Listen (bzw. Arrays) eintritt, die schon sortiert sind, kann man den Worst Case ganz einfach vermeiden: Man muss vor dem Aufruf von Quicksort die Elemente mischen!
Quicksort ist das schnellste vergleichsbasierte Sortierverfahren. Das liegt daran, dass es für Arrays in situ sortiert, d.h. es müssen keine neuen Datenstrukturen erzeugt werden. Das ist der entscheidende Vorteil von Quicksort gegenüber Mergesort.
Implementierung
für Listen
Quicksort-Implementierung für eine Liste (vgl. Schnittstellenbeschreibung Zentralabitur), die mit Objekten vom Typ Person gefüllt ist.
Diese Implementierung ist einfacher als die Array-Implementierung, dafür aber nicht so schnell, denn man muss ständig neue Listen erzeugen.
public List<Person> quicksort(List<Person> pList){
// leere Ergebnis-Liste erzeugen
List<Person> ergebnis = new ListWithViewer<Person>();
// Abbruchbedingung für die leere Liste
if(pList.isEmpty()){
return ergebnis;
}
// das erste Element der Liste als Pivot-Element festlegen
pList.toFirst();
Person pivot = pList.getContent();
// zum nächsten Element gehen
pList.next();
// die Listen links und rechts als leere Listen erzeugen
List<Person> links = new List<Person>();
List<Person> rechts = new List<Person>();
// pList durchlaufen und die Elemente mit pivot vergleichen:
// kleinere kommen nach links, die anderen nach rechts.
while(pList.hasAccess()){
Person p = pList.getContent();
if(p.getEinkommen() < pivot.getEinkommen()){
links.append(p);
}
else{
rechts.append(p);
}
pList.next();
}
// rekursive Aufrufe von quicksort für links und rechts
List<Person> linksSortiert = quicksort(links);
List<Person> rechtsSortiert = quicksort(rechts);
// die sortierten Teillisten und das Pivot-Element
// in der richtigen Reihenfolge an ergebnis anhängen
ergebnis.concat(linksSortiert);
ergebnis.append(pivot);
ergebnis.concat(rechtsSortiert);
// die ergebnis-Liste zurückgeben
return ergebnis;
}