Graph: Unterschied zwischen den Versionen
| (51 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Kategorie:Informatik]] | [[Kategorie:Informatik]] | ||
[[Kategorie:Informatik-Abitur]] | [[Kategorie:Informatik-Abitur]] | ||
[[Kategorie:Informatik-Q1]] | |||
[[Kategorie:Datenstrukturen(IF)]] | [[Kategorie:Datenstrukturen(IF)]] | ||
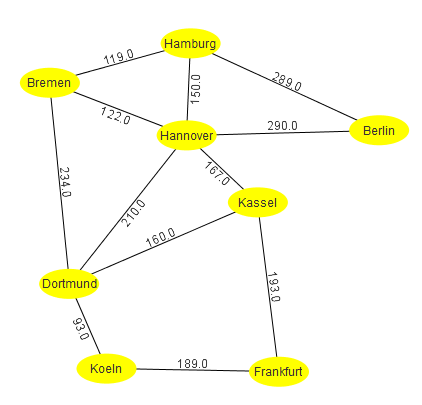
[[File:Graph_staedte_entfernungen.png|thumb|Graph für die Distanzen zwischen Städten |400px]] | |||
<font color='red'>'''nur relevant für den Leistungskurs!'''</font> | |||
Ein Graph ist in der Graphentheorie eine Struktur, die eine Menge von Objekten zusammen mit den zwischen diesen Objekten bestehenden Verbindungen repräsentiert. | Ein Graph ist in der Graphentheorie eine Struktur, die eine Menge von Objekten zusammen mit den zwischen diesen Objekten bestehenden Verbindungen repräsentiert. | ||
Die mathematischen Abstraktionen der Objekte werden dabei '''Knoten''' des Graphen genannt. Die paarweisen Verbindungen zwischen Knoten heißen '''Kanten'''. | |||
Ein Graph kann entweder als Graph, als '''Adjazenzliste''' oder als '''Adjazenzmatrix''' dargestellt werden. | |||
=Erklärvideos= | |||
* [https://youtu.be/bZLxTuG8cY0 Breiten- und Tiefendurchlauf: Theorie] | |||
* [https://youtu.be/2mHKVXy0xqo Breitendurchlauf: Implementierung] | |||
* [https://youtu.be/cdNonZrj_WE Tiefendurchlauf: Implementierung] | |||
=Fachbegriffe= | |||
Graph, Knoten, markieren, Kante, Gewicht, Traversierung, Breitendurchlauf, Tiefendurchlauf | |||
=Schnittstellenbeschreibung= | |||
[[Medium:Graph_Schnittstellen_Abitur_2018.pdf|Graph Schnittstellenbeschreibung (ab Abi 2018)]] | |||
==Adjazenzmatrix== | |||
Knoten und Kanten eines Graphen können in Form einer Matrix dargestellt werden. | |||
Die Matrix ist dabei spiegelsymmetrisch. | |||
Der oben dargestellte Graph hat folgende '''Adjazenzmatrix''': | |||
{| class="wikitable" | |||
|- | |||
!| ||Berlin || Bremen || Dortmund || Frankfurt || Hamburg || Hannover || Kassel || Koeln | |||
|- | |||
||<b>Berlin</b> || || || || || 289 || 290 || || | |||
|- | |||
||<b>Bremen</b> || || || 234 || || 119 || 122 || || | |||
|- | |||
||<b>Dortmund</b> || || 234 || || || || 210 || 160 || 93 | |||
|- | |||
||<b>Frankfurt</b>|| || || || || || || 193 || 189 | |||
|- | |||
||<b>Hamburg</b> || 289 || 119 || || || || 150 || || | |||
|- | |||
||<b>Hannover</b> || 290 || 122 || 210 || || 150 || || 167 || | |||
|- | |||
||<b>Kassel</b> || || || 160 || 193 || || 167 || || | |||
|- | |||
||<b>Koeln</b> || || || 93 || 189 || || || || | |||
|} | |||
TODO: Algorithmus zum Erzeugen eines Graphen aus einem 2D-Array (Adjazenzmatrix) | |||
==Adjazenzliste== | |||
Man kann die Informationen eines Graphen auch als Adjazenzliste darstellen. Das bietet sich z.B. an, wenn es in einem Graphen nur wenige Kanten gibt; dann ist die komplette Adjazenzmatrix Platzverschwendung. | |||
In der Adjazenzliste werden '''<u>links</u> von oben nach unten''' alle Knoten aufgeführt, z.B. in alphabetischer Reihenfolge; die Reihenfolge ist aber frei wählbar. | |||
<u>'''Nach rechts'''</u> werden alle Nachbarknoten des linken Knoten mit den zugehörigen Entfernungen eingetragen. Auch hier ist die Reihenfolge frei wählbar. | |||
Der oben dargestelle Graph hat folgende Adjazenzliste: | |||
<code> | |||
'''Berlin''' → Hamburg (289) → Hannover (290) | |||
↓ | |||
'''Bremen''' → Dortmund (234) → Hamburg (119) → Hannover (122) | |||
↓ | |||
'''Dortmund''' → Bremen (234) → Hannover (210) → Kassel (190) → Köln (93) | |||
↓ | |||
'''Frankfurt''' → Kassel (193) → Köln (189) | |||
↓ | |||
'''Hamburg''' → Berlin (289) → Bremen (119) → Hannover (150) | |||
↓ | |||
'''Hannover''' → Berlin (290) → Bremen (122) → Dortmund (210) → Hamburg (150) → Kassel (167) | |||
↓ | |||
'''Kassel''' → Dortmund (160) → Frankfurt (193) → Hannover (167) | |||
↓ | |||
'''Koeln''' → Dortmund (93) → Frankfurt (189) | |||
</code> | |||
==Traversierungen von Graphen== | ==Traversierungen von Graphen== | ||
Wie bei Bäumen gibt es auch bei Graphen viele Anwendungen, in denen ein Graph knotenweise durchlaufen werden muss. | Wie bei Bäumen gibt es auch bei Graphen viele Anwendungen, in denen ein Graph knotenweise durchlaufen werden muss. | ||
| Zeile 25: | Zeile 96: | ||
Der Tiefendurchlauf entspricht der [[Binärbaum#Beispiel:_preorder-Traversierung|Preorder-Traversierung eines Baumes]]. | Der Tiefendurchlauf entspricht der [[Binärbaum#Beispiel:_preorder-Traversierung|Preorder-Traversierung eines Baumes]]. | ||
====Beispiel:==== | |||
''Es gibt für jeden Startknoten mehrere mögliche Tiefendurchläufe, denn man kann sich bei den Nachbarknoten frei entscheiden, welchen man zuerst nimmt. In diesem Beispiel werden die Nachbarknoten immer nach alphabetischer Ordnung genommen.'' | |||
'''Tiefendurchlauf für den Startknoten Frankfurt''': | |||
''Zu Anfang kann man immer direkt weitergehen:'' | |||
Frankfurt -> Kassel -> Dortmund -> Bremen -> Hamburg -> Berlin -> Hannover | |||
''Von Hannover aus ist kein freier Knoten mehr erreichbar. Deswegen muss man jetzt in der Liste zurckgehen, bis man zu einem Knoten kommt, der noch einen freien Nachbarknoten hat. Das ist in diesem Fall '''Dortmund''' (der freie Nachbarknoten ist '''Koeln'''). Das heißt, Koeln wird als nächstes angehängt, und man würde von Köln aus weitersuchen (wenn es noch freie Knoten gäbe...) | |||
Ergebnis: | |||
'''Frankfurt -> Kassel -> Dortmund -> Bremen -> Hamburg -> Berlin -> Hannover -> Koeln''' | |||
====Implementierung==== | ====Implementierung==== | ||
Der Tiefendurchlauf durch einen Graphen wird am einfachsten rekursiv programmiert. | Der Tiefendurchlauf durch einen Graphen wird am einfachsten '''rekursiv''' programmiert. | ||
Voraussetzung: kein Knoten ist markiert! | |||
<code> | <code> | ||
public List tiefendurchlauf(Graph pGraph, | public List<Vertex> tiefendurchlauf(Graph pGraph, Vertex pNode){ | ||
List | List<Vertex> ergebnis = new List<>(); | ||
// | '''//Abbruchbedingung''' | ||
if(pNode.isMarked()){ | |||
return ergebnis; | |||
} | } | ||
return | |||
// pNode an die ergebnis-Liste anhaengen und markieren | |||
ergebnis.append(pNode); | |||
pNode.setMark(true); | |||
//Alle Nachbarn von pNode | |||
List<Vertex> nachbarn = pGraph.getNeighbours(pNode); | |||
//Nachbarn mit for-Schleife durchlaufen | |||
'''for(nachbarn.toFirst(); nachbarn.hasAccess(); nachbarn.next()){''' | |||
Vertex aktuellerNachbar = nachbarn.getContent(); | |||
'''//Rekursiver Aufruf''' | |||
List<Vertex> erg2 = <b><u>tiefendurchlauf(pGraph, aktuellerNachbar)</u></b>; | |||
ergebnis.concat(erg2); | |||
} | |||
return ergebnis; | |||
} | } | ||
</code> | </code> | ||
=== Breitendurchlauf=== | === Breitendurchlauf=== | ||
| Zeile 67: | Zeile 158: | ||
Im Binärbaum ist der Breitendurchlauf genau [[Binärbaum_(Methoden)#Levelorder|Levelorder]]. | Im Binärbaum ist der Breitendurchlauf genau [[Binärbaum_(Methoden)#Levelorder|Levelorder]]. | ||
== | ====Beispiel==== | ||
= | ''Beim Breitendurchlauf gibt es für jeden Startknoten mehrere Möglichkeiten, denn mann kann zwischen den Nachbarknoten wählen. Hier werden die Nachbarknoten immer in alphabetischer Reihenfolge betrachtet.'' | ||
'' | |||
''' | '''Breitendurchlauf für den Startknoten Frankfurt''' | ||
''Erst der Startknoten und seine Nachbarknoten:'' | |||
Frankfurt -> Kassel -> Koeln | |||
''Jetzt wird von den Nachbarknoten der erste genommen und dessen Nachbarknoten werden betrachtet:'' | |||
<b> | Frankfurt -> <b>Kassel</b> -> Koeln -> Dortmund -> Hannover | ||
''Der nächste Knoten in der Liste, der noch freie Nachbarknoten hat, ist Dortmund:'' | |||
Frankfurt -> Kassel -> Koeln -> <b>Dortmund</b> -> Hannover -> Bremen | |||
''Schließlich die Nachbarknoten von Hannover:'' | |||
'''Frankfurt -> Kassel -> Koeln -> Dortmund -> <b>Hannover</b> -> Bremen -> Berlin -> Hamburg | |||
''' | |||
</ | |||
''Beim Breitendurchlauf wird also zuerst die "nähere Umgebung" betrachtet.'' | |||
====Implementierung==== | ====Implementierung==== | ||
Die Implementierung setzt darauf auf, dass der Graph '''linearisiert''' wird: | |||
Man braucht eine <code>knotenListe</code>; in diese werden nach und nach alle Knoten des Graphen gemäß der Breitendurchlauf-Reihenfolge eingefügt. | |||
<code> | # zuerst wird der Startknoten als ''besucht'' markiert und in <code>knotenListe</code> eingefügt. | ||
# Dann wird <code>knotenListe</code> von Anfang bis Ende durchlaufen. Dabei passiert folgendes: | |||
## Für jeden Nachbarknoten des aktuellen Knoten wird überprüft, ob er schon ''besucht'' wurde. Wenn nein, dann wird er als ''besucht'' markiert und in <code>knotenListe</code> eingefügt. | |||
So wächst die <code>knotenListe</code> von einem Element (=dem Startknoten) beginnend immer weiter an, während sie durchlaufen wird. Die [[Schleife (Informatik)|Schleife]] kommt zum Ende, wenn alle Knoten eingefügt und als ''besucht'' gekennzeichnet sind. | |||
</code> | |||
''' | |||
<code> | <code> | ||
public List<Vertex> breitenDurchlauf(Graph pGraph, Vertex pStart){ | |||
List<Vertex> ergebnis = new List<Vertex>(); | |||
// alle Markierungen loeschen | |||
pGraph.setAllVertexMarks(false); | |||
pGraph.setAllEdgeMarks(false); | |||
// den Startknoten markieren und in ergebnis einfuegen | |||
// | '''pStart.setMark(true);''' | ||
'''ergebnis.append(pStart);''' | |||
// ergebnis durchlaufen: | |||
// ergebnis hat zu Anfang nur ein Element... | |||
// ... waechst dann aber immer weiter! | |||
'''for(ergebnis.toFirst(); ergebnis.hasAccess(); ergebnis.next()){''' | |||
Vertex aktuell = ergebnis.getContent(); | |||
List<Vertex> nachbarn = pGraph.getNeighbours(aktuell); | |||
// die Nachbarn mit einer Schleife durchlaufen | |||
'''for(nachbarn.toFirst(); nachbarn.hasAccess(); nachbarn.next()){''' | |||
Vertex aktuellerNachbar = nachbarn.getContent(); | |||
''' | // Wenn der aktuelleNachbar nicht markiert ist, | ||
// wird er zu ergebnis hinzugefuegt | |||
'''if(!aktuellerNachbar.isMarked()){''' | |||
Edge kante = pGraph.getEdge(aktuell, aktuellerNachbar); | |||
kante.setMark(true); | |||
aktuellerNachbar.setMark(true); | |||
'''ergebnis.append(aktuellerNachbar);''' | |||
} | |||
} // ende des Durchlaufs durch die Nachbarn. | |||
} // ende des Durchlaufs durch ergebnis | |||
return ergebnis; | |||
} | } | ||
</code> | |||
</code> | |||
== | == Backtracking: kürzeste Wege auf Graphen == | ||
siehe [[Backtracking]] | |||
== | == Dijkstra-Algorithmus: kürzeste Wege auf Graphen == | ||
siehe [[Dijkstra-Algorithmus]] | |||
=== | == Anwendungsbeispiele zu Graphen == | ||
=== | ===Minimaler Spannbaum=== | ||
siehe [[Minimaler Spannbaum]] | |||
Aktuelle Version vom 23. Januar 2022, 16:58 Uhr
nur relevant für den Leistungskurs!
Ein Graph ist in der Graphentheorie eine Struktur, die eine Menge von Objekten zusammen mit den zwischen diesen Objekten bestehenden Verbindungen repräsentiert. Die mathematischen Abstraktionen der Objekte werden dabei Knoten des Graphen genannt. Die paarweisen Verbindungen zwischen Knoten heißen Kanten.
Ein Graph kann entweder als Graph, als Adjazenzliste oder als Adjazenzmatrix dargestellt werden.
Erklärvideos
Fachbegriffe
Graph, Knoten, markieren, Kante, Gewicht, Traversierung, Breitendurchlauf, Tiefendurchlauf
Schnittstellenbeschreibung
Graph Schnittstellenbeschreibung (ab Abi 2018)
Adjazenzmatrix
Knoten und Kanten eines Graphen können in Form einer Matrix dargestellt werden. Die Matrix ist dabei spiegelsymmetrisch.
Der oben dargestellte Graph hat folgende Adjazenzmatrix:
| Berlin | Bremen | Dortmund | Frankfurt | Hamburg | Hannover | Kassel | Koeln | |
|---|---|---|---|---|---|---|---|---|
| Berlin | 289 | 290 | ||||||
| Bremen | 234 | 119 | 122 | |||||
| Dortmund | 234 | 210 | 160 | 93 | ||||
| Frankfurt | 193 | 189 | ||||||
| Hamburg | 289 | 119 | 150 | |||||
| Hannover | 290 | 122 | 210 | 150 | 167 | |||
| Kassel | 160 | 193 | 167 | |||||
| Koeln | 93 | 189 |
TODO: Algorithmus zum Erzeugen eines Graphen aus einem 2D-Array (Adjazenzmatrix)
Adjazenzliste
Man kann die Informationen eines Graphen auch als Adjazenzliste darstellen. Das bietet sich z.B. an, wenn es in einem Graphen nur wenige Kanten gibt; dann ist die komplette Adjazenzmatrix Platzverschwendung.
In der Adjazenzliste werden links von oben nach unten alle Knoten aufgeführt, z.B. in alphabetischer Reihenfolge; die Reihenfolge ist aber frei wählbar.
Nach rechts werden alle Nachbarknoten des linken Knoten mit den zugehörigen Entfernungen eingetragen. Auch hier ist die Reihenfolge frei wählbar.
Der oben dargestelle Graph hat folgende Adjazenzliste:
Berlin → Hamburg (289) → Hannover (290)
↓
Bremen → Dortmund (234) → Hamburg (119) → Hannover (122)
↓
Dortmund → Bremen (234) → Hannover (210) → Kassel (190) → Köln (93)
↓
Frankfurt → Kassel (193) → Köln (189)
↓
Hamburg → Berlin (289) → Bremen (119) → Hannover (150)
↓
Hannover → Berlin (290) → Bremen (122) → Dortmund (210) → Hamburg (150) → Kassel (167)
↓
Kassel → Dortmund (160) → Frankfurt (193) → Hannover (167)
↓
Koeln → Dortmund (93) → Frankfurt (189)
Traversierungen von Graphen
Wie bei Bäumen gibt es auch bei Graphen viele Anwendungen, in denen ein Graph knotenweise durchlaufen werden muss. Die Traversierungsverfahren ähneln denen bei Bäumen, berücksichtigen allerdings noch die speziellen Gegebenheiten von Graphen, nämlich:
- Graphenknoten können mehr als zwei Nachbarn haben
- Graphen können Querverbindungen und "Kreise" enthalten
Tiefendurchlauf
Erläuterung
Beim Tiefendurchlauf (engl. Depth First Search - DFS) durch einen Baum nimmt man ausgehend von einem Startknoten den ersten Nachbarknoten. Von diesem nimmt man wieder den ersten Nachbarknoten usw. Wenn man dann in eine Sackgasse gerät, geht man eine Stufe zurück und nimmt den nächsten Nachbarknoten. Natürlich werden Knoten, die man schon besucht hat, nicht noch einmal berücksichtigt.
Der Tiefendurchlauf entspricht der Preorder-Traversierung eines Baumes.
Beispiel:
Es gibt für jeden Startknoten mehrere mögliche Tiefendurchläufe, denn man kann sich bei den Nachbarknoten frei entscheiden, welchen man zuerst nimmt. In diesem Beispiel werden die Nachbarknoten immer nach alphabetischer Ordnung genommen.
Tiefendurchlauf für den Startknoten Frankfurt:
Zu Anfang kann man immer direkt weitergehen:
Frankfurt -> Kassel -> Dortmund -> Bremen -> Hamburg -> Berlin -> Hannover
Von Hannover aus ist kein freier Knoten mehr erreichbar. Deswegen muss man jetzt in der Liste zurckgehen, bis man zu einem Knoten kommt, der noch einen freien Nachbarknoten hat. Das ist in diesem Fall Dortmund (der freie Nachbarknoten ist Koeln). Das heißt, Koeln wird als nächstes angehängt, und man würde von Köln aus weitersuchen (wenn es noch freie Knoten gäbe...)
Ergebnis:
Frankfurt -> Kassel -> Dortmund -> Bremen -> Hamburg -> Berlin -> Hannover -> Koeln
Implementierung
Der Tiefendurchlauf durch einen Graphen wird am einfachsten rekursiv programmiert.
Voraussetzung: kein Knoten ist markiert!
public List<Vertex> tiefendurchlauf(Graph pGraph, Vertex pNode){
List<Vertex> ergebnis = new List<>();
//Abbruchbedingung
if(pNode.isMarked()){
return ergebnis;
}
// pNode an die ergebnis-Liste anhaengen und markieren
ergebnis.append(pNode);
pNode.setMark(true);
//Alle Nachbarn von pNode
List<Vertex> nachbarn = pGraph.getNeighbours(pNode);
//Nachbarn mit for-Schleife durchlaufen
for(nachbarn.toFirst(); nachbarn.hasAccess(); nachbarn.next()){
Vertex aktuellerNachbar = nachbarn.getContent();
//Rekursiver Aufruf
List<Vertex> erg2 = tiefendurchlauf(pGraph, aktuellerNachbar);
ergebnis.concat(erg2);
}
return ergebnis;
}
Breitendurchlauf
Der Breitendurchlauf (engl. breadth first search - BFS) ist eine Methode, um alle Knoten eines Graphen aufzuzählen.
Erläuterung
Mit dem Breitendurchlauf werden die Knoten in folgender Reihenfolge aufgezählt:
- zuerst der Startknoten,
- dann die Nachbarknoten des Startknotens, d.h. alle Knoten, die vom Startknoten aus über eine Kante erreichbar sind.
- dann die Knoten, die vom Startknoten aus mit zwei Kanten erreichbar sind.
- usw.
Knoten, die schon einmal aufgezählt wurden, werden natürlich nicht wieder aufgezählt.
Im Binärbaum ist der Breitendurchlauf genau Levelorder.
Beispiel
Beim Breitendurchlauf gibt es für jeden Startknoten mehrere Möglichkeiten, denn mann kann zwischen den Nachbarknoten wählen. Hier werden die Nachbarknoten immer in alphabetischer Reihenfolge betrachtet.
Breitendurchlauf für den Startknoten Frankfurt
Erst der Startknoten und seine Nachbarknoten:
Frankfurt -> Kassel -> Koeln
Jetzt wird von den Nachbarknoten der erste genommen und dessen Nachbarknoten werden betrachtet:
Frankfurt -> Kassel -> Koeln -> Dortmund -> Hannover
Der nächste Knoten in der Liste, der noch freie Nachbarknoten hat, ist Dortmund:
Frankfurt -> Kassel -> Koeln -> Dortmund -> Hannover -> Bremen
Schließlich die Nachbarknoten von Hannover:
Frankfurt -> Kassel -> Koeln -> Dortmund -> Hannover -> Bremen -> Berlin -> Hamburg
Beim Breitendurchlauf wird also zuerst die "nähere Umgebung" betrachtet.
Implementierung
Die Implementierung setzt darauf auf, dass der Graph linearisiert wird:
Man braucht eine knotenListe; in diese werden nach und nach alle Knoten des Graphen gemäß der Breitendurchlauf-Reihenfolge eingefügt.
- zuerst wird der Startknoten als besucht markiert und in
knotenListeeingefügt. - Dann wird
knotenListevon Anfang bis Ende durchlaufen. Dabei passiert folgendes:- Für jeden Nachbarknoten des aktuellen Knoten wird überprüft, ob er schon besucht wurde. Wenn nein, dann wird er als besucht markiert und in
knotenListeeingefügt.
- Für jeden Nachbarknoten des aktuellen Knoten wird überprüft, ob er schon besucht wurde. Wenn nein, dann wird er als besucht markiert und in
So wächst die knotenListe von einem Element (=dem Startknoten) beginnend immer weiter an, während sie durchlaufen wird. Die Schleife kommt zum Ende, wenn alle Knoten eingefügt und als besucht gekennzeichnet sind.
public List<Vertex> breitenDurchlauf(Graph pGraph, Vertex pStart){
List<Vertex> ergebnis = new List<Vertex>();
// alle Markierungen loeschen
pGraph.setAllVertexMarks(false);
pGraph.setAllEdgeMarks(false);
// den Startknoten markieren und in ergebnis einfuegen
pStart.setMark(true);
ergebnis.append(pStart);
// ergebnis durchlaufen:
// ergebnis hat zu Anfang nur ein Element...
// ... waechst dann aber immer weiter!
for(ergebnis.toFirst(); ergebnis.hasAccess(); ergebnis.next()){
Vertex aktuell = ergebnis.getContent();
List<Vertex> nachbarn = pGraph.getNeighbours(aktuell);
// die Nachbarn mit einer Schleife durchlaufen
for(nachbarn.toFirst(); nachbarn.hasAccess(); nachbarn.next()){
Vertex aktuellerNachbar = nachbarn.getContent();
// Wenn der aktuelleNachbar nicht markiert ist,
// wird er zu ergebnis hinzugefuegt
if(!aktuellerNachbar.isMarked()){
Edge kante = pGraph.getEdge(aktuell, aktuellerNachbar);
kante.setMark(true);
aktuellerNachbar.setMark(true);
ergebnis.append(aktuellerNachbar);
}
} // ende des Durchlaufs durch die Nachbarn.
} // ende des Durchlaufs durch ergebnis
return ergebnis;
}
Backtracking: kürzeste Wege auf Graphen
siehe Backtracking
Dijkstra-Algorithmus: kürzeste Wege auf Graphen
siehe Dijkstra-Algorithmus
Anwendungsbeispiele zu Graphen
Minimaler Spannbaum
siehe Minimaler Spannbaum