Dijkstra-Algorithmus: Unterschied zwischen den Versionen
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 74: | Zeile 74: | ||
<b>Klasse <code>DijkstraTest</code>:</b> | <b>Klasse <code>DijkstraTest</code>:</b> | ||
<code> | <code> | ||
package _test; | package _test; | ||
| Zeile 95: | Zeile 95: | ||
'''public List<DijkstraInfo> dijkstraAlgorithmus(String sStart)'''{ | '''public List<DijkstraInfo> dijkstraAlgorithmus(String sStart)'''{ | ||
roteListe = new ListWithViewer<DijkstraInfo>(); | |||
gelbeListe = new ListWithViewer<DijkstraInfo>(); | |||
Vertex vStart = graph.getVertex(sStart); | |||
DijkstraInfo dStart = new DijkstraInfo(vStart,0,null); | |||
dStart.setDistanz(0); | |||
gelbeListe.append(dStart); | |||
while(! gelbeListe.isEmpty()){ | |||
gelbeListe.toFirst(); | |||
DijkstraInfo neuerRoterDI = gelbeListe.getContent(); | |||
gelbeListe.remove(); | |||
roteListe.append(neuerRoterDI); | |||
Vertex neuerRoterV = neuerRoterDI.getVertex(); | |||
neuerRoterV.setMark(true); | |||
double distanzBisNeuerRoter = neuerRoterDI.getDistanz(); | |||
List<Vertex> nachbarn = graph.getNeighbours(neuerRoterV); | |||
for(nachbarn.toFirst();nachbarn.hasAccess();nachbarn.next()){ | |||
Vertex nachbarV = nachbarn.getContent(); | |||
if(! nachbarV.isMarked()){ | |||
Edge e = graph.getEdge(neuerRoterV, nachbarV); | |||
DijkstraInfo neuDI = new DijkstraInfo(nachbarV,distanzBisNeuerRoter+e.getWeight(),neuerRoterV); | |||
inGelbeListeUpdaten(neuDI); | |||
} | |||
} | |||
} | |||
return roteListe; | |||
} | } | ||
| Zeile 246: | Zeile 245: | ||
} | } | ||
} | } | ||
</code> | </code> | ||
| Zeile 252: | Zeile 251: | ||
<b>Klasse <code>DijkstraInfo</code>:</b> | <b>Klasse <code>DijkstraInfo</code>:</b> | ||
<code> | <code> | ||
package graph; | package graph; | ||
public class DijkstraInfo{ | public class DijkstraInfo{ | ||
private Vertex vertex; | |||
private double distanz; | |||
private Vertex vorgaenger; | |||
public DijkstraInfo(Vertex pVertex, double pDistanz, Vertex pVorgaenger){ | |||
this.vertex = pVertex; | |||
this.distanz = pDistanz; | |||
this.vorgaenger = pVorgaenger; | |||
} | |||
public Vertex getVertex(){ | |||
return vertex; | |||
} | |||
public double getDistanz() { | |||
return distanz; | |||
} | |||
public void setDistanz(double distanz) { | |||
this.distanz = distanz; | |||
} | |||
public Vertex getVorgaenger() { | |||
return vorgaenger; | |||
} | |||
public void setVorgaenger(Vertex vorgaenger) { | |||
this.vorgaenger = vorgaenger; | |||
} | |||
public String toString() { | |||
if(vorgaenger != null){ | |||
return vertex.getID() + ", " + distanz + ", Vorg.: " + vorgaenger.getID(); | |||
} | |||
else{ | |||
return vertex.getID() + ", " + distanz + ", Vorg.: ---"; | |||
} | |||
} | |||
} | } | ||
</code> | |||
</code> | |||
Aktuelle Version vom 23. Januar 2022, 17:00 Uhr
Mit Hilfe des Dijkstra-Algorithmus kann man für einen Startknoten die kürzesten Wege zu allen anderen Knoten des Graphen bestimmen.
Der Dijkstra-Algorithmus ist wesentlich effizienter als die Suche nach einem kürzesten Weg mithilfe von Backtracking
Der Dijkstra-Algorithmus bezieht sich auf die Datenstruktur Graph.
Fachbegriffe
Dijkstra-Algorithmus, rote Liste, gelbe Liste
Idee des Dijkstra-Algorithmus
Notwendige Datenstrukturen
- Für jeden Knoten wird der Vorgänger und ein Wert
distanzgespeichert;distanzgibt die bisher beste gefundene Distanz zum Startknoten an. - gelbe Liste: In dieser Liste werden Knoten gespeichert, für die schon ein Distanzwert vorliegt, deren Distanz zum Startknoten aber noch nicht abschließend festgelegt werden konnte. Die Knoten erscheinen in der gelben Liste gemäß ihrem Distanzwert, und zwar in aufsteigender Reihenfolge.
- rote Liste: Man braucht eine Liste, in der alle Knoten gespeichert werden, deren Distanz zum Startknoten abschließend festgestellt wurde.
Algorithmus
- Die Distanz des Startknoten wird auf 0 gesetzt; der von allen anderen Knoten auf unendlich.
- Der Startknoten wird in die rote Liste eingefügt.
- Alle Nachbarknoten des Startknotens werden in die gelbe Liste eingefügt, und zwar gemäß ihrer Distanz zum Startknoten.
- Die folgenden Schritte laufen jetzt so lange, bis die gelbe Liste leer ist:
- den ersten Knoten aus der gelben Liste (im folgenden
ersterGelber) entnehmen und in die rote Liste einfügen. Denn die Distanz dieses Knotens ist endgültig geklärt. - für alle Nachbarknoten von
ersterGelberüberprüft man:- wenn sie noch nicht in der gelben Liste sind: Distanz berechnen (=Distanz von
ersterGelberplus Kantenlänge vonersterGelber) und dann in die gelbe Liste hinzufügen (=gemäß der Distanz einfügen) - wenn sie schon in der gelben Liste sind: Überprüfen, ob die Distanz von
ersterGelberplus Kantenlänge kleiner ist als die bisher gespeicherte Distanz: Dann hat man eine bessere Route gefunden! Die Distanz des Nachbarknoten wird dann entsprechend verbessert, wodurch sich seine Position in der gelben Liste verbessert.
- wenn sie noch nicht in der gelben Liste sind: Distanz berechnen (=Distanz von
- den ersten Knoten aus der gelben Liste (im folgenden
Kürzester Weg für einen beliebigen Knoten
Die Distanz kann man direkt aus dem Knoten auslesen.
Den kürzesten Weg von einem beliebigen Knoten zum Startknoten kann man jetzt angeben, indem man sich von dem Knoten aus immer zum nächsten Vorgänger hangelt, bis mn schließlich beim Startknoten angekommen ist.
Beispiel
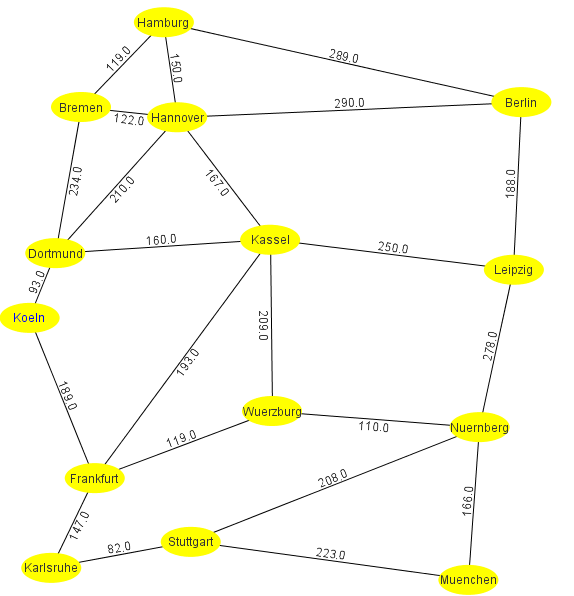
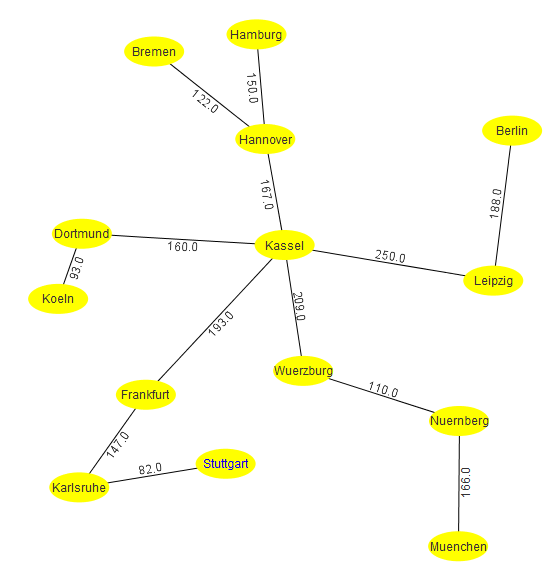
Für den Startknoten Kassel sind die ersten Schritte des Dijkstra-Algorithmus die folgenden.
- Die rote Liste' ist fett geschrieben und ist von oben nach unten zu lesen.
- Die gelbe Liste ist jeweils von links nach rechts zu lesen.
- Veränderungen in der gelben Liste sind unterstrichen.
In der gelben Liste wird in Klammern die aktuelle Distanz zum Startknoten und der Vorgängerknoten (als Nummernschild) angegeben.
- Kassel (0, --): Dortmund (160, KS), Hannover (167, KS), Frankfurt (193, KS), Wuerzburg (209, KS), Leipzig (250, KS)
- Dortmund (160, KS): Hannover (167, KS), Frankfurt (193, KS), Wuerzburg (209, KS), Leipzig (250, KS), Koeln (253, DO), Bremen (394, DO)
- Hannover (167, KS): Frankfurt (193, KS), Wuerzburg (209, KS), Leipzig (250, KS), Koeln (253, DO), Bremen (289, H), Hamburg (317, H), Berlin (457, H)
- Frankfurt (193, KS): Wuerzburg (209, KS), Leipzig (250, KS), Koeln (253, DO), Bremen (289, H), Hamburg (317, H), Karlsruhe (340, F), Berlin (457, H)
- Wuerzburg (209, KS): Leipzig (250, KS), Koeln (253, DO), Bremen (289, H), Hamburg (317, H), Nuernberg (319, WÜ), Karlsruhe (340, F), Berlin (457, H)
- Leipzig (250, KS): Koeln (253, DO), Bremen (289, H), Hamburg (317, H), Nuernberg (319, WÜ), Berlin (438, L)
- Koeln (253, DO): Bremen (289, H), Hamburg (317, H), Nuernberg (319, WÜ), Karlsruhe (340, F), Berlin (438, L)
- Bremen (289, H): Hamburg (317, H), Nuernberg (319, WÜ), Karlsruhe (340, F), Berlin (438, L)
- Hamburg (317, H): Nuernberg (319, WÜ), Karlsruhe (340, F), Berlin (438, L)
- Nuernberg (319, WÜ): Karlsruhe (340, F), Berlin (438, L), Muenchen (485, N), Stuttgart (527, N)
- Karlsruhe (340, F): Stuttgart (422, KA), Berlin (438, L), Muenchen (485, N)
- Stuttgart (422, KA): Berlin (438, L), Muenchen (485, N)
- Berlin (438, L): Muenchen (485, N)
- Muenchen (485, N)
Den kürzesten Weg von Kassel nach Stuttgart findet man jetzt, indem man in der roten Liste Stuttgart sucht und dann in der roten Liste "rückwärts" geht:
Stuttgart (422, KA) -> Karlsruhe (340, F) -> Frankfurt (193, KS) -> Kassel (0, --)
Implementierung
Diese Implementierung umfasst zwei Klassen:
DijkstraTestDijkstraInfo
Die Klasse DijkstraTest enthält eine (lange...) Methode initGraph, damit man das Ganze auch testen kann.
Klasse DijkstraTest:
package _test;
import linear.List;
import graph.DijkstraInfo;
import graph.Edge;
import graph.Vertex;
import gui.GUI;
import graph.GraphWithViewer;
import linear.ListWithViewer;
public class DijkstraTest {
private GraphWithViewer graph;
private List<DijkstraInfo> gelbeListe;
private List<DijkstraInfo> roteListe;
public DijkstraTest(){
initMap();
}
public List<DijkstraInfo> dijkstraAlgorithmus(String sStart){
roteListe = new ListWithViewer<DijkstraInfo>();
gelbeListe = new ListWithViewer<DijkstraInfo>();
Vertex vStart = graph.getVertex(sStart);
DijkstraInfo dStart = new DijkstraInfo(vStart,0,null);
dStart.setDistanz(0);
gelbeListe.append(dStart);
while(! gelbeListe.isEmpty()){
gelbeListe.toFirst();
DijkstraInfo neuerRoterDI = gelbeListe.getContent();
gelbeListe.remove();
roteListe.append(neuerRoterDI);
Vertex neuerRoterV = neuerRoterDI.getVertex();
neuerRoterV.setMark(true);
double distanzBisNeuerRoter = neuerRoterDI.getDistanz();
List<Vertex> nachbarn = graph.getNeighbours(neuerRoterV);
for(nachbarn.toFirst();nachbarn.hasAccess();nachbarn.next()){
Vertex nachbarV = nachbarn.getContent();
if(! nachbarV.isMarked()){
Edge e = graph.getEdge(neuerRoterV, nachbarV);
DijkstraInfo neuDI = new DijkstraInfo(nachbarV,distanzBisNeuerRoter+e.getWeight(),neuerRoterV);
inGelbeListeUpdaten(neuDI);
}
}
}
return roteListe;
}
/**
* Sorgt dafuer, dass dInfo gemaess seiner Distanz
* die richtige Position in der gelbe Liste bekommt.
* Falls dInfo noch gar nicht in gelbeListe enthalten ist,
* dann wird dInfo an der richtigen Stelle eingefuegt.
*/
private void inGelbeListeUpdaten(DijkstraInfo dInfo) {
boolean inserted = false;
gelbeListe.toFirst();
while(gelbeListe.hasAccess()){
DijkstraInfo aktuell = gelbeListe.getContent();
if(aktuell.getDistanz() >= dInfo.getDistanz()){
gelbeListe.insert(dInfo);
inserted = true;
break;
}
if(aktuell.getVertex()== dInfo.getVertex()){
// gibt es schon - mit kleinerer Distanz!
gelbeListe.toFirst();
return;
}
gelbeListe.next();
}
if(inserted){
// ggf. taucht der Knoten nochmal in der Liste auf!
// dann muss er entfernt werden!
while(gelbeListe.hasAccess()){
DijkstraInfo aktuell = gelbeListe.getContent();
if(aktuell.getVertex() == dInfo.getVertex()){
gelbeListe.remove();
break;
}
gelbeListe.next();
}
}
else{
// der Knoten wurde noch nicht eingefuegt!
gelbeListe.append(dInfo);
}
gelbeListe.toFirst();
}
public void initMap(){
graph = new GraphWithViewer();
Vertex kiel = new Vertex("Kiel");
graph.addVertex(kiel);
Vertex luebeck = new Vertex("Luebeck");
graph.addVertex(luebeck);
Vertex hamburg = new Vertex("Hamburg");
graph.addVertex(hamburg);
Vertex berlin = new Vertex("Berlin");
graph.addVertex(berlin);
Vertex bremen = new Vertex("Bremen");
graph.addVertex(bremen);
Vertex hannover = new Vertex("Hannover");
graph.addVertex(hannover);
Vertex dortmund = new Vertex("Dortmund");
graph.addVertex(dortmund);
Vertex bochum = new Vertex("Bochum");
graph.addVertex(bochum);
Vertex koeln = new Vertex("Koeln");
graph.addVertex(koeln);
Vertex bonn = new Vertex("Bonn");
graph.addVertex(bonn);
Vertex mainz = new Vertex("Mainz");
graph.addVertex(mainz);
Vertex frankfurt = new Vertex("Frankfurt");
graph.addVertex(frankfurt);
Vertex kassel = new Vertex("Kassel");
graph.addVertex(kassel);
Vertex wuerzburg = new Vertex("Wuerzburg");
graph.addVertex(wuerzburg);
Vertex leipzig = new Vertex("Leipzig");
graph.addVertex(leipzig);
Vertex nuernberg = new Vertex("Nuernberg");
graph.addVertex(nuernberg);
Vertex stuttgart = new Vertex("Stuttgart");
graph.addVertex(stuttgart);
Vertex muenchen = new Vertex("Muenchen");
graph.addVertex(muenchen);
Vertex karlsruhe = new Vertex("Karlsruhe");
graph.addVertex(karlsruhe);
graph.addEdge(new Edge(kiel, hamburg, 97));
graph.addEdge(new Edge(kiel, luebeck, 84));
graph.addEdge(new Edge(luebeck, hamburg, 74));
graph.addEdge(new Edge(luebeck, berlin, 284));
graph.addEdge(new Edge(berlin, hamburg, 289));
graph.addEdge(new Edge(hamburg, bremen, 119));
graph.addEdge(new Edge(bremen, hannover, 122));
graph.addEdge(new Edge(hannover, hamburg, 150));
graph.addEdge(new Edge(berlin, hannover, 290));
graph.addEdge(new Edge(berlin, leipzig, 188));
graph.addEdge(new Edge(hannover, kassel, 167));
graph.addEdge(new Edge(leipzig, kassel, 250));
graph.addEdge(new Edge(kassel, dortmund, 160));
graph.addEdge(new Edge(dortmund, bremen, 234));
graph.addEdge(new Edge(dortmund, hannover, 210));
graph.addEdge(new Edge(dortmund, bochum, 22));
graph.addEdge(new Edge(dortmund, koeln, 107));
graph.addEdge(new Edge(koeln, bochum, 82));
graph.addEdge(new Edge(koeln, bonn, 29));
graph.addEdge(new Edge(bonn, mainz, 169));
graph.addEdge(new Edge(frankfurt, mainz, 45));
graph.addEdge(new Edge(frankfurt, kassel, 193));
graph.addEdge(new Edge(leipzig, nuernberg, 278));
graph.addEdge(new Edge(kassel, wuerzburg, 209));
graph.addEdge(new Edge(wuerzburg, nuernberg, 110));
graph.addEdge(new Edge(wuerzburg, frankfurt, 119));
graph.addEdge(new Edge(nuernberg, muenchen, 166));
graph.addEdge(new Edge(muenchen, stuttgart, 223));
graph.addEdge(new Edge(nuernberg, stuttgart, 208));
graph.addEdge(new Edge(stuttgart, karlsruhe, 82));
graph.addEdge(new Edge(karlsruhe, frankfurt, 147));
graph.addEdge(new Edge(frankfurt, koeln, 189));
graph.switchToISOMLayout();
}
public static void main(String[] args) {
DijkstraTest dt = new DijkstraTest();
new GUI(dt);
}
}
Klasse DijkstraInfo:
package graph;
public class DijkstraInfo{
private Vertex vertex;
private double distanz;
private Vertex vorgaenger;
public DijkstraInfo(Vertex pVertex, double pDistanz, Vertex pVorgaenger){
this.vertex = pVertex;
this.distanz = pDistanz;
this.vorgaenger = pVorgaenger;
}
public Vertex getVertex(){
return vertex;
}
public double getDistanz() {
return distanz;
}
public void setDistanz(double distanz) {
this.distanz = distanz;
}
public Vertex getVorgaenger() {
return vorgaenger;
}
public void setVorgaenger(Vertex vorgaenger) {
this.vorgaenger = vorgaenger;
}
public String toString() {
if(vorgaenger != null){
return vertex.getID() + ", " + distanz + ", Vorg.: " + vorgaenger.getID();
}
else{
return vertex.getID() + ", " + distanz + ", Vorg.: ---";
}
}
}