Binärbaum: Unterschied zwischen den Versionen
K (Akaibel verschob die Seite Allgemeiner Binärbaum ab Abi 2017 nach Binärbaum) |
|||
| (8 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
[[File:Ahnenbaum.png|thumb|Ahnenbaum: Justus und seine Vorfahren|300px]] | [[File:Ahnenbaum.png|thumb|Ahnenbaum: Justus und seine Vorfahren|300px]] | ||
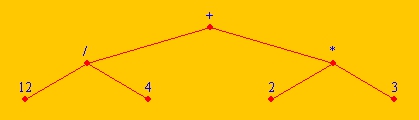
[[File:Strukturbaum.jpg|thumb|Binärer Strukturbaum (12/4)+(2*3) |300px]] | [[File:Strukturbaum.jpg|thumb|Binärer Strukturbaum (12/4)+(2*3) |300px]] | ||
'''<font color="red">Diese Seite entspricht dem Abi 17 (und folgenden)</font>''' | |||
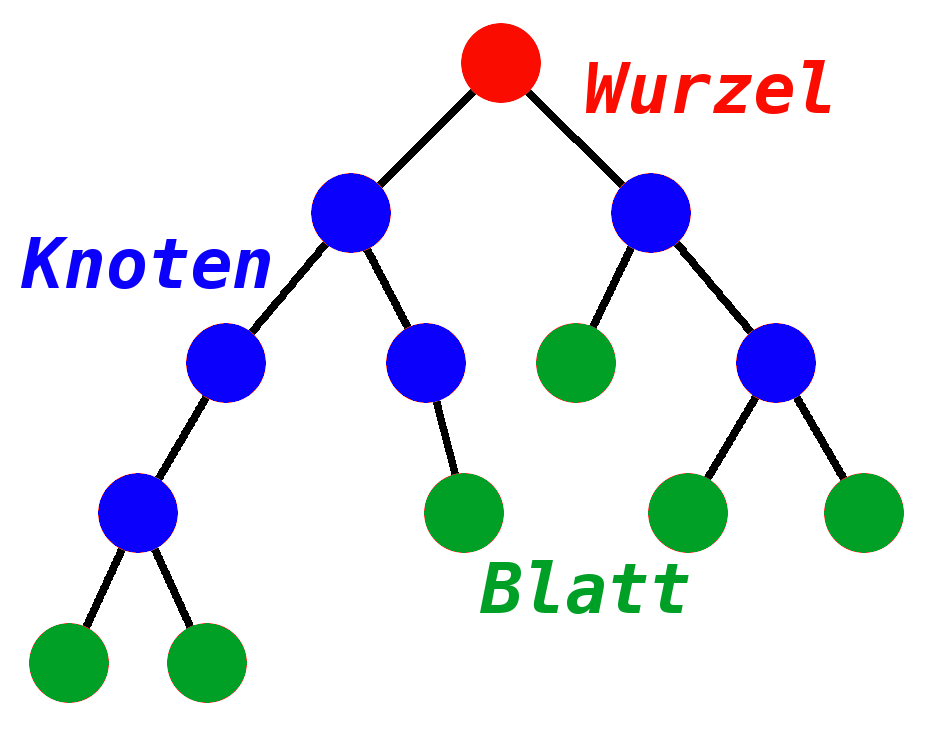
* Ein Binärbaum ist ein gewurzelter Baum, bei dem jeder Knoten keine (auch Blatt genannt), eine oder maximal zwei Teilbäume besitzt. | * Ein Binärbaum ist ein gewurzelter Baum, bei dem jeder Knoten keine (auch Blatt genannt), eine oder maximal zwei Teilbäume besitzt. | ||
* Als Spezialfall des Binärbaumes gibt es den [[ | * Als Spezialfall des Binärbaumes gibt es den [[Binärer Suchbaum|Binären Suchbaum]]. | ||
* Wie '''Methoden''' für Binärbäume implementiert werden können, wird in folgendem Artikel erklärt: [[Binärbaum_(Methoden) | * Wie '''Methoden''' für Binärbäume implementiert werden können, wird in folgendem Artikel erklärt: [[Binärbaum_(Methoden)]] | ||
=Erklärvideos= | |||
* [https://youtu.be/XrsfRh5S2Vw Prinzip der Traversierungen ''Preorder'' und ''Inorder''] | |||
* [https://youtu.be/SjniaclqvFs Levelorder-Traversierung: Prinzip und Implementierung] | |||
=Fachbegriffe= | |||
Kante, Knoten, Wurzel, Blatt, Tiefe, Traversierung (Inorder, Preorder, Levelorder), Rekursion, Abbruchbedingung, rekursiver Aufruf, Sachlogik, Rahmenmethode | |||
= Schnittstelle des Zentralabiturs = | = Schnittstelle des Zentralabiturs = | ||
[[Medium:Dokumentation2017_BinaryTree.pdf|Binärbaum Schnittstelle des Zentralabiturs(PDF)]] | [[Medium:Dokumentation2017_BinaryTree.pdf|Binärbaum Schnittstelle des Zentralabiturs(PDF)]] | ||
| Zeile 20: | Zeile 31: | ||
Traversierungen sind Methoden, um alle Knoten eines Baumes in eine Liste zu übertragen. | Traversierungen sind Methoden, um alle Knoten eines Baumes in eine Liste zu übertragen. | ||
[https://youtu.be/XrsfRh5S2Vw Erklärvideo: Prinzip der Traversierungen ''Preorder'' und ''Inorder''] | |||
==Prinzip== | ==Prinzip== | ||
* Preorder: '''Wurzel''' -> Links -> Rechts | * Preorder: '''Wurzel''' -> Links -> Rechts | ||
| Zeile 35: | Zeile 47: | ||
'''Implementierung:''' | '''Implementierung:''' | ||
<code> | <code> | ||
public List<String> preorder(BinaryTree<String> pTree) | public List<String> preorder(BinaryTree<String> pTree) | ||
{ | { | ||
| Zeile 45: | Zeile 57: | ||
// Wurzelelement auslesen | // Wurzelelement auslesen | ||
String | String wurzel = pTree.getContent(); | ||
// rekursiver Aufruf: erst fuer links, dann fuer rechts | // rekursiver Aufruf: erst fuer links, dann fuer rechts | ||
| Zeile 52: | Zeile 64: | ||
// das ergebnis zusammenbauen | // das ergebnis zusammenbauen | ||
ergebnis.append( | ergebnis.append(wurzel); | ||
ergebnis.concat(linkeListe); | ergebnis.concat(linkeListe); | ||
ergebnis.concat(rechteListe); | ergebnis.concat(rechteListe); | ||
return ergebnis; | return ergebnis; | ||
} | } | ||
</code> | </code> | ||
==Levelorder-Traversierung (nur LK)== | ==Levelorder-Traversierung (nur LK)== | ||
[[File:Ahnenbaum.png|thumb|Ahnenbaum: Beispiel für Levelorder: Ahnenbaum|300px]] | [[File:Ahnenbaum.png|thumb|Ahnenbaum: Beispiel für Levelorder: Ahnenbaum|300px]] | ||
[https://youtu.be/SjniaclqvFs Erklärvideo: Prinzip und Implementierung der Levelorder-Traversierung] | |||
Bei der Levelorder-Traversierung wird ein Binärbaum '''schichtenweise''' durchlaufen, d.h.: | Bei der Levelorder-Traversierung wird ein Binärbaum '''schichtenweise''' durchlaufen, d.h.: | ||
* erst die Wurzel | * erst die Wurzel | ||
| Zeile 97: | Zeile 112: | ||
==Implementierung== | ==Implementierung== | ||
<code> | <code> | ||
public class Personenverwaltung{ | public class Personenverwaltung{ | ||
| Zeile 137: | Zeile 152: | ||
return ergebnis; | return ergebnis; | ||
} | } | ||
</code> | </code> | ||
Aktuelle Version vom 18. Januar 2023, 15:45 Uhr
Diese Seite entspricht dem Abi 17 (und folgenden)
- Ein Binärbaum ist ein gewurzelter Baum, bei dem jeder Knoten keine (auch Blatt genannt), eine oder maximal zwei Teilbäume besitzt.
- Als Spezialfall des Binärbaumes gibt es den Binären Suchbaum.
- Wie Methoden für Binärbäume implementiert werden können, wird in folgendem Artikel erklärt: Binärbaum_(Methoden)
Erklärvideos
- Prinzip der Traversierungen Preorder und Inorder
- Levelorder-Traversierung: Prinzip und Implementierung
Fachbegriffe
Kante, Knoten, Wurzel, Blatt, Tiefe, Traversierung (Inorder, Preorder, Levelorder), Rekursion, Abbruchbedingung, rekursiver Aufruf, Sachlogik, Rahmenmethode
Schnittstelle des Zentralabiturs
Binärbaum Schnittstelle des Zentralabiturs(PDF)
Wichtiger Hinweis:
In der Schnittstelle des Zentralabiturs wird immer davon ausgegangen, dass unter den "sichtbaren" Knoten von Bäumen noch leere Knoten sind. Das hat den enormen Vorteil, dass man beim rekursiven Durchlauf durch einen Baum mit isEmpty() abbrechen kann.
Traversierung
Traversierungen sind Methoden, um alle Knoten eines Baumes in eine Liste zu übertragen.
Erklärvideo: Prinzip der Traversierungen Preorder und Inorder
Prinzip
- Preorder: Wurzel -> Links -> Rechts
- Inorder: Links -> Wurzel -> Rechts
Für den Inorder-Durchlauf kann man den Baum "von links nach rechts" lesen.
Inorder gibt in Bäumen mit Suchbaumstruktur die Knoten sortiert zurück. - Postorder: Links -> Rechts -> Wurzel
- Levelorder: Der Baum wird "schichtenweise" in eine Liste übertragen.
Preorder, Inorder und Postorder sind Tiefendurchläufe. Levelorder dagegen ist ein Breitendurchlauf.
Beispiel: preorder-Traversierung
Bei der preorder-Traversierung handelt es sich (genauso wie bei inorder und postorder) um eine Tiefensuche. D.h. es wird erst ein Teil des Baums bis ganz nach unten durchsucht, bevor die anderen Zweige drankommen.
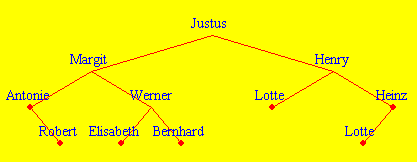
Preorder-Traversierung des Ahnenbaums:
Justus, Margit, Antonie, Robert, Werner, Elisabeth, Bernhard, Henry, Lotte, Heinz, Lotte
Implementierung:
public List<String> preorder(BinaryTree<String> pTree)
{
List<String> ergebnis = new List<>();
// Abbruchbedingung
if (pTree.isEmpty()){
return ergebnis;
}
// Wurzelelement auslesen
String wurzel = pTree.getContent();
// rekursiver Aufruf: erst fuer links, dann fuer rechts
List<String> linkeListe = preorder(pTree.getLeftTree());
List<String> rechteListe = preorder(pTree.getRightTree());
// das ergebnis zusammenbauen
ergebnis.append(wurzel);
ergebnis.concat(linkeListe);
ergebnis.concat(rechteListe);
return ergebnis;
}
Levelorder-Traversierung (nur LK)
Erklärvideo: Prinzip und Implementierung der Levelorder-Traversierung
Bei der Levelorder-Traversierung wird ein Binärbaum schichtenweise durchlaufen, d.h.:
- erst die Wurzel
- dann die Wurzeln der beiden Teilbäume
- usw.
Für den Ahnenbaum ergibt sich folgende Levelorder-Reihenfolge:
Justus, Margit, Henry, Antonie, Werner, Lotte, Heinz, Robert, Elisabeth, Bernhard, Lotte.
D.h. man erhält die Vorfahren generationsweise.
Zur Implementierungsstrategie siehe Linearisierung im Artikel Binärbaum_(Methoden).
weitere Methoden
Implementierungen von weiteren Methoden finden sich hier:
Binärbaum_(Methoden) ab Abi 2017
Binärbäume, die Objekte enthalten
In den Beispielen oben sind in Binärbäumen jeweils nur Objekte vom Typ String oder vom Typ int enthalten.
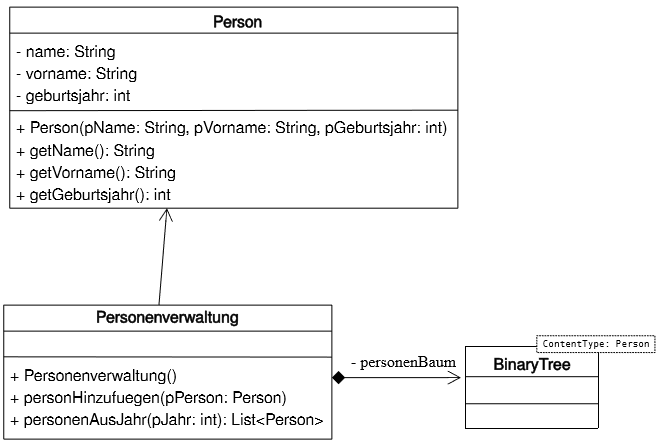
Häufig enthalten Binärbäume aber auch Objekte von selbstdefinierten Klassen. Wie man damit umgeht, soll anhand eines Binärbaumes dargestellt werden, der mit Objekten der Klasse Person gefüllt ist (vgl. Implementationsdiagramm rechts).
Beispiel: Suchen nach Geburtsjahrgang
Zu implementieren ist für die Klasse Personenverwaltung eine Methode personenAusJahr, der ein Jahr übergeben wird, und die dann aus dem Attribut personenBaum alle Personen dieses Jahrganges heraussucht und in einer Liste zurückgibt.
Die gewünschte Methode ist hier eine Rahmenmethode, die ihrerseits eine (private) rekursive Methode aufruft.
Rahmenmethode
Häufig gibt es den folgenden Fall:
- Ein Attribut einer Klasse muss rekursiv durchsucht werden, wie z.B. oben das Attribut
personenBaum. - Die gewünschte Methode ist aber nicht rekursiv ist (wie z.B. die Methode
public List personenAusJahr(int pGeburtsjahr)).
Dann macht man die gewünschte Methode zur Rahmenmethode, die ihrerseits eine private rekursive Methode aufruft.
Implementierung
public class Personenverwaltung{
// Attribut zur Verwaltung der Personen
private BinaryTree<Person> personenBaum;
// *** Konstruktor
public Personenverwaltung(){
// hier wird personenBaum initialisiert
// und mit Personen gefuellt
}
// Rahmenmethode
public List<Person> personenAusJahr(int pGeburtsjahr){
List<Person> ergebnis = personenAusJahr(personenBaum, pGeburtsjahr);
return ergebnis;
}
// rekursive Methode
private List<Person> personenAusJahr(BinaryTree<Person> pTree, int pGeburtsjahr){
List<Person> ergebnis = new List<>();
//Abbruchbedingung: leerer Baum
if(pTree.isEmpty()){
return ergebnis;
}
// die Wurzel des Baumes auslesen
// und in ein Objekt vom Typ Person konvertieren
Person wurzelPerson = pTree.getContent();
// Sachlogik: Vergleich des Geburtsjahres der wurzelPerson mit pGeburtsjahr
if(wurzelPerson.getGeburtsjahr() == pGeburtsjahr){
ergebnis.append(wurzelPerson);
}
// rekursive Aufrufe
List<Person> ergebnisLinks = personenAusJahr(pTree.getLeftTree(), pGeburtsjahr);
List<Person> ergebnisRechts = personenAusJahr(pTree.getRightTree(), pGeburtsjahr);
// die Ergebnisse anhängen
ergebnis.concat(ergebnisLinks);
ergebnis.concat(ergebnisRechts);
return ergebnis;
}