Aktuelle Version vom 3. März 2024, 17:48 Uhr

Der Diffie-Hellmann-Schlüsseltausch ermöglicht es zwei Kommunikationspartnern einen geheimen Schlüssel zu vereinbaren.

Das Besondere dabei ist, dass mögliche Angreifer die gesamte Kommunikation mithören können, aber trotzdem nicht an den Schlüssel kommen.

Verfahren

Die beiden Kommunikationspartner (Alice und Bob) einigen sich auf eine Primzahl p und eine Primitivwurzel g modulo p.

Diese beiden Zahlen können öffentlich sein, d.h. auch mögliche Angreifer (Eve) dürfen sie erfahren.

Jetzt läuft das Verfahren wie folgt ab:

a,b,K sind privat; g,p,A,B sind öffentlich

Alice	Kommunikation (belauscht von Eve!)	Bob
---	Alice und Bob einigen sich auf p und g	---
Alice denkt sich eine geheime Zahl a aus. (a muss kleiner als p sein.)	---	Bob denkt sich eine geheime Primzahl b aus. (b muss kleiner als p sein.)
Alice berechnet A = g^a mod p	---	Bob berechnet B = g^b mod p
---	Alice schickt A an Bob. Bob schickt B an Alice.	---
Alice berechnet K = B^a mod p und hat den Schlüssel K!	---	Bob berechnet K = A^b mod p und hat ebenfalls den Schlüssel K!
---	Eve kann aus p, g, A und B den Schlüssel K nicht berechnen!	---

Beispiel

Alice	Kommunikation (belauscht von Eve!)	Bob
---	Alice und Bob einigen sich auf p = 13 und g = 2	---
Alice denkt sich eine geheime Zahl aus: a = 5. (a muss kleiner als p sein)	---	Bob denkt sich eine geheime Zahl aus: b = 8. (b muss kleiner als p sein.)
Alice berechnet A = g^a mod p A = 2⁵ mod 13 = 32 mod 13 = 6	---	Bob berechnet B = g^b mod p B = 2⁸ mod 13 = 256 mod 13 = 9
---	Alice schickt A = 6 an Bob. Bob schickt B = 9 an Alice.	---
Alice berechnet K = B^a mod p K = 9⁵ mod 13 = 59049 mod 13 = 3 und hat den Schlüssel K = 3!	---	Bob berechnet K = A^b mod p K = 6^8 mod 13 = 1679616 mod 13 = 3 und hat den Schlüssel K = 3!
---	Eve kann aus p = 13, g = 2, A = 6 und B = 9 den Schlüssel K nicht berechnen!	---

Taschenrechner / Online-Rechner

Mit dem Casio-Taschenrechner kommt man am einfachsten so zum Modulo-Rechnen:

OPTN -> F6 -> F4 -> F6 -> F4
Eingabe dann z.B.: MOD(27,6)
Dann müsste 3 rauskommen.

Der Taschenrechner hat allerdings Probleme, modulo für große Zahlen zu berechnen.

Das kann man VIEL BESSER online machen!

Folgende Online-Rechner sind geeignet:

web2.0rechner.de.
(Modulo ist 2nd ÷ )

PowerMod-Calculator
Den braucht man, wenn auch der web2.0rechner überfordert ist, z.B. für 123456789^123456789 mod 987654321
allgemein: Basis ^ Exponent mod Modulo

Primitiv-Wurzel-Rechner
Zum Suchen von Primitivwurzeln.

Warum funktioniert das?

Alices Berechnug für K ist: K = B^a mod p = (g^b)^a mod p = g^ab mod p
Bobs Berechnung für K ist: K = A^b mod p = (g^a)^b mod p = g^ba mod p = g^ab mod p
Also haben Alice und Bob den gleichen Schlüssel!

Allgemeine Anforderungen an die Verschlüsselungsfunktion

Allgemein gesprochen muss die Verschlüsselungsfunktion kommutativ sein, d.h. f_a(f_b(x)) = f_b(f_a(x)).

Das ist wichtig, damit Alice und Bob den gleichen Schlüssel erhalten!

Die Exponentialfunktion modulo p ist kommutativ, wie oben gezeigt.

Außerdem muss die Verschlüsselungsfunktion eine Einwegfunktion sein, d.h. die Umkehrung der Rechnung muss unmöglich oder mindestens sehr zeitintensiv sein.

Das ist wichtig, damit man nicht aus den öffentlichen Teilen der Kommunikation die privaten Werte von Alice und Bob errechnen kann.

Dass die Exponentialfunktion modulo p eine Einwegfunktion ist, ist mathematisch bewiesen; siehe Warum ist das sicher?

Warum ist das sicher?

Um aus p, g, A und B den geheimen Schlüssel K (oder die geheimen Primzahlen a und b) zu ermitteln, muss Alice den sog. "diskreten Logarithmus" bilden
d.h. sie muss eine Zahl x finden, so dass g^x mod p = A.
Das erfordert für große Zahlen eine sehr lange Rechendauer; man kann sogar angeben, wie groß die Zahlen sein müssen, damit Eve mit aller Rechenleistung der Welt 10 Jahre, 100 Jahre oder 1000 Jahre braucht...

Mehr Details zur Sicherheit bei wikipedia

Praxis

In der Praxis nimmt man für p, g, a und b Zahlen mit mehreren hundert Stellen.

Man-In-The-Middle-Attack

Man-In-The-Middle-Attack auf Diffie-Hellman

Der Diffie-Hellmann-Schlüsseltausch ist anfällig für die Man-In-The-Middle-Attack.

D.h. wenn sich Mallory unbemerkt in den Schlüsselaustausch "einklinkt", indem sie Alice vorspiegelt, sie sei Bob und Bob vorspiegelt, sie sei Alice, dann kann Mallory mit jeder Seite einen Schlüssel vereinbaren - und Alice und Bob denken, sie hätten miteinander einen Schlüssel vereinbart. (Dabei haben beide jeweils nur einen Schlüssel mit dem bösen Mallory vereinbart!)

Details dazu bei wikipedia

Veranschaulichung: Mischen von Farben

Das Diffie-Hellman-Verfahren wird häufig durch ein Farbmisch-Verfahren veranschaulicht.

Man-In-The-Middle-Attack auf Diffie-Hellman

@@ Zeile 13: / Zeile 13: @@
 Jetzt läuft das Verfahren wie folgt ab:
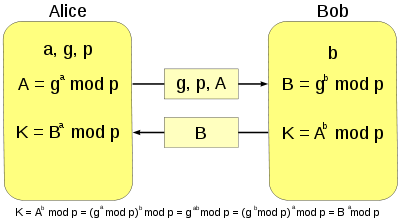
+[[File:Diffie-Hellman-Schlüsselaustausch.png|thumb|a,b,K sind privat; g,p,A,B sind öffentlich|400px]]
 {| class="wikitable"
@@ Zeile 21: / Zeile 23: @@
 | --- || Alice und Bob einigen sich auf '''p''' und '''g''' || ---
 |-
-| Alice denkt sich eine geheime Primzahl '''a''' aus. || --- || Bob denkt sich eine geheime Primzahl '''b''' aus.
+| Alice denkt sich eine geheime Zahl '''a''' aus.<br>(a muss kleiner als p sein.) || --- || Bob denkt sich eine geheime Primzahl '''b''' aus.<br>(b muss kleiner als p sein.)
 |-
-| Alice berechnet '''A''' = g^a mod p || --- || Bob berechnet '''B''' = g^b mod p
+| Alice berechnet '''A''' = g<sup>a</sup> mod p || --- || Bob berechnet '''B''' = g<sup>b</sup> mod p
 |-
 | --- || Alice schickt '''A''' an Bob. <br>Bob schickt '''B''' an Alice.|| ---
 |-
-| Alice berechnet '''K''' = B^a mod p<br>und hat den Schlüssel '''K'''! || --- || Bob berechnet '''K''' = A^b mod p<br>und hat ebenfalls den Schlüssel '''K'''!
+| Alice berechnet '''K''' = B<sup>a</sup> mod p<br>und hat den Schlüssel '''K'''! || --- || Bob berechnet '''K''' = A<sup>b</sup> mod p<br>und hat ebenfalls den Schlüssel '''K'''!
 |-
 | --- || Eve kann aus p, g, A und B <br>den Schlüssel '''K''' <u>nicht</u> berechnen! || ---
@@ Zeile 40: / Zeile 42: @@
 | --- || Alice und Bob einigen sich auf  '''p = 13''' und '''g = 2''' || ---
 |-
-| Alice denkt sich eine geheime Primzahl aus: '''a = 5'''. || --- || Bob denkt sich eine geheime Primzahl '''b = 8'''.
+| Alice denkt sich eine geheime Zahl aus: '''a = 5'''.<br>(a muss kleiner als p sein) || --- || Bob denkt sich eine geheime Zahl aus: '''b = 8'''.<br>(b muss kleiner als p sein.)
 |-
-| Alice berechnet '''A''' = g^a mod p <br> '''A''' = 2^5 mod 13 = 32 mod 13 = '''6'''|| --- || Bob berechnet '''B''' = g^b mod p <br> '''B''' = 2^8 mod 13 = 256 mod 13 = '''9'''
+| Alice berechnet '''A''' = g<sup>a</sup> mod p <br> '''A''' = 2<sup>5</sup> mod 13 = 32 mod 13 = '''6'''|| --- || Bob berechnet '''B''' = g<sup>b</sup> mod p <br> '''B''' = 2<sup>8</sup> mod 13 = 256 mod 13 = '''9'''
 |-
 | --- || Alice schickt '''A = 6''' an Bob. <br>Bob schickt '''B = 9''' an Alice.|| ---
 |-
-| Alice berechnet '''K''' = B^a mod p<br>'''K''' = 9^5 mod 13 = 59049 mod 13 = '''3'''<br>und hat den Schlüssel '''K = 3'''! || --- || Bob berechnet '''K''' = A^b mod p<br>'''K''' = 6^8 mod 13 = 1679616 mod 13 = '''3''' <br>und hat ebenfalls den Schlüssel '''K'''!
+| Alice berechnet '''K''' = B<sup>a</sup> mod p<br>'''K''' = 9<sup>5</sup> mod 13 = 59049 mod 13 = '''3'''<br>und hat den Schlüssel '''K = 3'''! || --- || Bob berechnet '''K''' = A<sup>b</sup> mod p<br>'''K''' = 6^8 mod 13 = 1679616 mod 13 = '''3''' <br>und hat den Schlüssel '''K = 3'''!
 |-
-| --- || Eve kann aus p = 13, g = 2,  A = 6 und B = 9 <br>den Schlüssel '''K''' nicht</u> berechnen! || ---
+| --- || Eve kann aus p = 13, g = 2,  A = 6 und B = 9 <br>den Schlüssel '''K''' <u>nicht</u> berechnen! || ---
 |}
+== Taschenrechner / Online-Rechner ==
+Mit dem Casio-Taschenrechner kommt man am einfachsten so zum Modulo-Rechnen:
+* <code>OPTN -> F6 -> F4 -> F6 -> F4</code>
+* Eingabe dann z.B.: <code>MOD(27,6)</code><br/>''Dann müsste 3 rauskommen.''
+Der Taschenrechner hat allerdings Probleme, modulo für große Zahlen zu berechnen.
+'''Das kann man VIEL BESSER online machen!'''
+Folgende Online-Rechner sind geeignet:
+* '''[http://web2.0rechner.de/ web2.0rechner.de]'''.<br/>''(Modulo ist '''<font size="4"><code>2nd</code>  <code>&divide;</code></font>   ''')''
+* '''[https://www.omnicalculator.com/math/power-modulo PowerMod-Calculator]'''<br/>Den braucht man, wenn auch der web2.0rechner überfordert ist, z.B. für 123456789^123456789 mod 987654321<br/>allgemein: Basis '''^''' Exponent '''mod''' Modulo <br/>
+* '''[https://services.informatik.hs-mannheim.de/KryptoLern/primitive_wurzel.php?p=29&start=8&cnt=12&x= Primitiv-Wurzel-Rechner]'''<br/>Zum Suchen von Primitivwurzeln.
+=Warum funktioniert das?=
+* Alices Berechnug für K ist: K = B<sup>a</sup> mod p = (g<sup>b</sup>)<sup>a</sup> mod p = g<sup>ab</sup> mod p
+* Bobs Berechnung für K ist: K = A<sup>b</sup> mod p = (g<sup>a</sup>)<sup>b</sup> mod p = g<sup>ba</sup> mod p = g<sup>ab</sup> mod p
+* Also haben Alice und Bob den gleichen Schlüssel!
+==Allgemeine Anforderungen an die Verschlüsselungsfunktion==
+Allgemein gesprochen muss die Verschlüsselungsfunktion '''kommutativ''' sein, d.h. f<sub>a</sub>(f<sub>b</sub>(x)) = f<sub>b</sub>(f<sub>a</sub>(x)).
+Das ist wichtig, damit Alice und Bob den gleichen Schlüssel erhalten!
+Die Exponentialfunktion modulo p ist kommutativ, wie oben gezeigt.
+Außerdem muss die Verschlüsselungsfunktion eine '''Einwegfunktion''' sein, d.h. die Umkehrung der Rechnung muss unmöglich oder mindestens sehr zeitintensiv sein.
+Das ist wichtig, damit man nicht aus den öffentlichen Teilen der Kommunikation die privaten Werte von Alice und Bob errechnen kann.
+Dass die Exponentialfunktion modulo p eine Einwegfunktion ist, ist mathematisch bewiesen; siehe [[Diffie-Hellmann-Schlüsseltausch#Warum ist das sicher?|Warum ist das sicher?]]
+=Warum ist das sicher?=
+* Um aus p, g, A und B den geheimen Schlüssel K (oder die geheimen Primzahlen a und b) zu ermitteln, muss Alice den sog. ''"diskreten Logarithmus"'' bilden <br>d.h. sie muss eine Zahl '''x''' finden, so dass g<sup>'''x'''</sup> mod p = A.
+* Das erfordert für große Zahlen eine sehr lange Rechendauer; man kann sogar angeben, wie groß die Zahlen sein müssen, damit Eve mit aller Rechenleistung der Welt 10 Jahre, 100 Jahre oder 1000 Jahre braucht...
+Mehr Details zur Sicherheit bei [http://de.wikipedia.org/wiki/Diffie-Hellman-Schlüsselaustausch#Diffie-Hellman-Problem wikipedia]
+=Praxis=
+In der Praxis nimmt man für p, g, a und b Zahlen mit mehreren hundert Stellen.
+=Man-In-The-Middle-Attack=
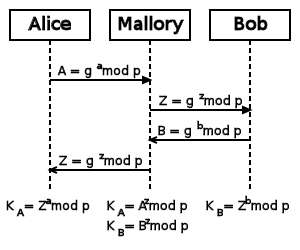
+[[File:Diffie-Hellman-Man-In-The-Middle-Attack.png|thumb|Man-In-The-Middle-Attack auf Diffie-Hellman|300px]]
+Der Diffie-Hellmann-Schlüsseltausch ist anfällig für die Man-In-The-Middle-Attack.
+D.h. wenn sich Mallory unbemerkt in den Schlüsselaustausch "einklinkt", indem sie Alice vorspiegelt, sie sei Bob und Bob vorspiegelt, sie sei Alice, dann kann Mallory mit jeder Seite einen Schlüssel vereinbaren - und Alice und Bob denken, sie hätten miteinander einen Schlüssel vereinbart. (Dabei haben beide jeweils nur einen Schlüssel mit dem bösen Mallory vereinbart!)
+Details dazu bei [http://de.wikipedia.org/wiki/Diffie-Hellman-Schlüsselaustausch#Man-in-the-Middle-Angriff wikipedia]
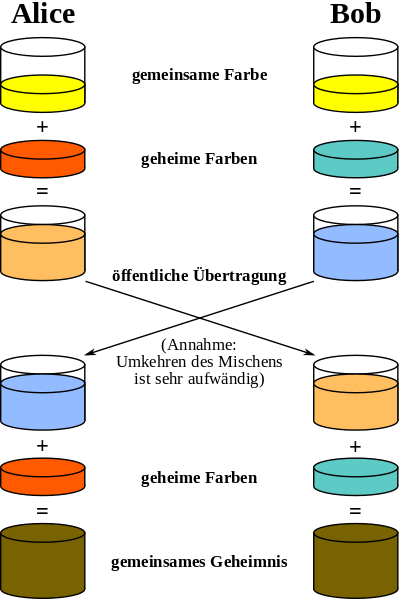
+=Veranschaulichung: Mischen von Farben=
+Das Diffie-Hellman-Verfahren wird häufig durch ein Farbmisch-Verfahren veranschaulicht.
+[[File:Diffie-Hellman-Farben.png|left|Man-In-The-Middle-Attack auf Diffie-Hellman|399px]]

Diffie-Hellmann-Schlüsseltausch: Unterschied zwischen den Versionen