Binärer Suchbaum: Unterschied zwischen den Versionen
| Zeile 142: | Zeile 142: | ||
=Suchen (search)= | =Suchen (search)= | ||
Die Klasse <code>BinarySearchTree</code> bietet die Methode <code>search</code>, um Elemente im Baum zu suchen. | Die Klasse <code>BinarySearchTree</code> bietet die Methode <code>search</code>, um Elemente im Baum zu suchen. | ||
Ist das Element enthalten, wird es zurückgegeben. Dies mag auf den ersten Blick sinnlos erscheinen, bietet aber die Möglichkeit, ein Objekt zu einem bestimmten Attributwert zu holen, indem man zunächst ein Dummy-Objekt erstellt, das mit dem gesuchten Objekt nur in diesem Attibutwert übereinstimmt und sich damit das zugehörige ''wirkliche Objekt'' aus dem <code>BinaryTree</code> sucht. (''Die übeerschriebene Methode <code>isEqual()</code> darf natürlich nur Gleichheit genau auf diesem Attribut testen!'') | |||
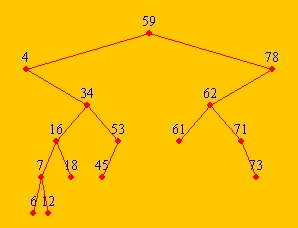
Binäre Suchbäume haben den Vorteil, dass man in ihnen sehr schnell Elemente suchen kann: Man muss nicht den ganzen Baum zu durchsuchen, sondern kann - ausgehend von der Wurzel - einen Pfad bis zum Blatt abgehen. Je nachdem, ob das gesuchte Element kleiner oder größer ist als der gerade betrachtete Knoten, biegt man rechts (bzw. links) ab. (''In der Abiturklasse ist allerdings kein klassischer [[Binärbaum (Methoden) ab Abi 2017#Durchlaufen eines Pfades|Pfaddurchlauf]] (mit while-Schleife etc.) umgesetzt, sondern eine rekursive Variante gewählt worden, die aber auch nur den einen notwendigen Pfad durchläuft.'') | Binäre Suchbäume haben den Vorteil, dass man in ihnen sehr schnell Elemente suchen kann: Man muss nicht den ganzen Baum zu durchsuchen, sondern kann - ausgehend von der Wurzel - einen Pfad bis zum Blatt abgehen. Je nachdem, ob das gesuchte Element kleiner oder größer ist als der gerade betrachtete Knoten, biegt man rechts (bzw. links) ab. (''In der Abiturklasse ist allerdings kein klassischer [[Binärbaum (Methoden) ab Abi 2017#Durchlaufen eines Pfades|Pfaddurchlauf]] (mit while-Schleife etc.) umgesetzt, sondern eine rekursive Variante gewählt worden, die aber auch nur den einen notwendigen Pfad durchläuft.'') | ||
Version vom 10. August 2016, 07:23 Uhr
Definition
Ein binärer Suchbaum ist ein Binärbaum mit einer zusätzlichen Eigenschaft:
- die Elemente im linken Teilbaum sind kleiner als die Wurzel; die Elemente im rechten Teilbaum sind größer als die Wurzel.
- Diese Eigenschaft gilt auch für alle Teilbäume eines binären Suchbaumes.
Wie kleiner bzw. größer definiert werden, hängt dabei vom Anwendungszusammenhang ab; bei Personen kann z.B. das Alter oder die alphabetische Ordnung des Nachnamens das wesentliche Ordnungskriterium sein.
Eigenschaften eines Suchbaumes
- In Binären Suchbäumen kann man sehr schnell Elemente finden (daher der Name...); vgl. Suchen von Elementen in einem Binären Suchbaum
- Der Inorder-Durchlauf (Links -> Wurzel -> Rechts) eines Suchbaumes ergibt genau die alphabetische Ordnung. (Zu den verschiedenen Durchlaufarten durch Binärbäume: s. Traversierung von Binärbäumen)
Schnittstelle des Zentralabiturs
Schnittstelle BinarySearchTree (PDF)
Erläuterungen zur Schnittstelle
Die Schnittstelle des Zentralabiturs besteht aus zwei Klassen:
BinarySearchTreeist der eigentliche binäre Suchbaum.ComparableCOntent: In einenBinarySearchTreekönnen nur Objekte eingefügt werden, die die SchnittstelleComparableContentimplementieren.ComparableContenterzwingt die Implementierung der MethodenisEqual,isGreaterundisLess. Dadurch wird festgelegt, wie Objekte in den Suchbaum einsortiert werden.
Beispiel: Verwendung von BinarySearchTree und ComparableContent
Objekte der Klasse Buch sollen in einen binären Suchbaum eingefügt bzw. nach bestimmten Titeln gesucht werden. Dabei soll das Ordnungskriterium die alphabetische Ordnung nach dem Titel sein.
Dafür muss die Klasse Buch die Schnittstelle ComparableContent implementieren und die Methoden isEqual, isGreater und isLess so überschreiben, dass die Bücher nach dem Titel verglichen werden.
public class Buch implements ComparableContent<Buch>{
private String titel;
private int regalNr;
public Buch(String pTitel, int pRegalNr){
titel = pTitel;
regalNr = pRegalNr;
}
public int getRegalNr() {
return regalNr;
}
public void setRegalNr(int regalNr) {
this.regalNr = regalNr;
}
public String getTitel() {
return titel;
}
public boolean isEqual(Buch pContent) {
Buch pBuch = pContent;
boolean ergebnis = false;
if(titel.equals(pBuch.getTitel())){
ergebnis = true;
}
return ergebnis;
}
public boolean isLess(Buch pContent) {
Buch pBuch = pContent;
boolean ergebnis = false;
if(titel.compareTo(pBuch.getTitel())<0){
ergebnis = true;
}
return ergebnis;
}
public boolean isGreater(Buch pContent) {
Buch pBuch = pContent;
boolean ergebnis = false;
if(titel.compareTo(pBuch.getTitel())>0){
ergebnis = true;
}
return ergebnis;
}
}
Jetzt können z.B. in einer Klasse Bibliothek Objekte der Klasse Buch in einen BinarySearchTree eingefügt werden:
public class Bibliothek{
//hier werden die Buecher gespeichert
BinarySearchTree<Buch> buecherBaum;
public Bibliothek(){
buecherBaum = new BinarySearchTree<Buch>();
}
public void uebertrageListeInBaum(List<Buch> buecherListe){
for(buecherListe.toFirst(); buecherListe.hasAccess(); buecherListe.next()){
Buch aktuellesBuch = buecherListe.getContent();
buecherBaum.insert(aktuellesBuch);
}
}
public Buch suche(String pTitel){
// man muss erst ein Dummy-Buch erzeugen
// nach dem kann man dann suchen
Buch dummyBuch = new Buch(pTitel, -1);
Buch ergebnis = buecherBaum.search(dummyBuch);
return ergebnis;
}
}
Erläuterungen zur Methode public Buch suche(String pTitel):
Die Implementierung sieht auf den ersten Blick etwas eigenwillig aus, ist aber die einfachste und schnellste. Warum wird das so gemacht?
- In Objekten vom Typ
BinarySearchTree<Buch>kann man nur nach Objekten vom TypBuchsuchen. - D.h. man muss erst ein
dummyBucherstellen, das den gewünschten Titel trägt. - Da
Buchdie SchnittstelleComparableContentimplementiert, kann man mithilfe vondummyBuchdie Methodesearchaufrufen. searchgibt dann das "richtige" gesuchte Buch zurück.- WICHTIG:
ergebnisist das "richtige" Buch;dummyBuchwurde nur dafür erstellt, damit man nach einem Titel suchen kann!
Implementationsdiagramm
!!!TODO: Ändern, ist nun (Abi 2017) anders umgesetzt!!!
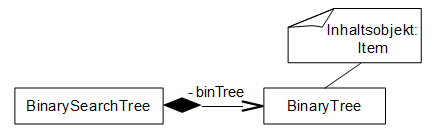
- Der BinarySearchTree hat ein Objekt
binTreevom TypBinaryTree, um die Knoten zu speichern. binTreeenthält nur Objekte vom TypItem.
Item: Java-Quellcode
Wenn Item als Interface aufgefasst wird (Begründung: s.o.), dann ist die Implementierung denkbar einfach:
public interface Item {
public boolean isEqual(Item pItem);
public boolean isLess(Item pItem);
public boolean isGreater(Item pItem);
}
- Die Methoden werden in
Itemnur deklariert, aber nicht implementiert! - Jede Klasse, die Item implementiert (Syntax:
public MyClass implements Item), muss diese drei Methoden überschreiben und eine Implementierung anbieten.
Suchen (search)
Die Klasse BinarySearchTree bietet die Methode search, um Elemente im Baum zu suchen.
Ist das Element enthalten, wird es zurückgegeben. Dies mag auf den ersten Blick sinnlos erscheinen, bietet aber die Möglichkeit, ein Objekt zu einem bestimmten Attributwert zu holen, indem man zunächst ein Dummy-Objekt erstellt, das mit dem gesuchten Objekt nur in diesem Attibutwert übereinstimmt und sich damit das zugehörige wirkliche Objekt aus dem BinaryTree sucht. (Die übeerschriebene Methode isEqual() darf natürlich nur Gleichheit genau auf diesem Attribut testen!)
Binäre Suchbäume haben den Vorteil, dass man in ihnen sehr schnell Elemente suchen kann: Man muss nicht den ganzen Baum zu durchsuchen, sondern kann - ausgehend von der Wurzel - einen Pfad bis zum Blatt abgehen. Je nachdem, ob das gesuchte Element kleiner oder größer ist als der gerade betrachtete Knoten, biegt man rechts (bzw. links) ab. (In der Abiturklasse ist allerdings kein klassischer Pfaddurchlauf (mit while-Schleife etc.) umgesetzt, sondern eine rekursive Variante gewählt worden, die aber auch nur den einen notwendigen Pfad durchläuft.)
Implementierung (LK)
public ContentType search(ContentType pContent) {
if (this.isEmpty() || pContent == null) {
// Abbrechen, da es kein Element zu suchen gibt.
return null;
} else {
ContentType content = this.getContent();
if (pContent.isLess(content)) {
// Element wird im linken Teilbaum gesucht.
return this.getLeftTree().search(pContent);
} else if (pContent.isGreater(content)) {
// Element wird im rechten Teilbaum gesucht.
return this.getRightTree().search(pContent);
} else if (pContent.isEqual(content)) {
// Element wurde gefunden.
return content;
} else {
// Dieser Fall sollte nicht auftreten.
return null;
}
}
}
Einfügen (insert)
Um Elemente in einen binären Suchbaum einzufügen, muss man ausgehend von der Wurzel einen Pfad bis zu einem leeren Knoten abgehen. Je nachdem, ob das gesuchte Element kleiner oder größer ist als der gerade betrachtete Knoten, biegt man rechts (bzw. links) ab. Sobald man einen leeren Knoten gefunden hat, ist man an der richtigen Stelle, wo man das Element einfügen kann.
Implementierung (LK)
public void insert(Item pItem) {
// eine Referenz auf das Attribut binTree (vom Typ BinaryTree) deklarieren
// in diesem Attribut werden die Knoten des BinarySearchTree verwaltet!
BinaryTree bt = binTree;
// so lange weitergehen, bis man auf einen leeren Knoten stoesst
while(!bt.isEmpty()){
Item wurzelItem = bst.getObject();
// ueberpruefen, ob man das richtige gefunden hat
if(wurzelItem.isEqual(pItem)){
// es ist nichts zu tun!
return;
}
// weiter nach unten gehen
if(pItem.isLess(wurzelItem)){
bt = bt.getLeftTree();
}
else{
bt = bt.getRightTree();
}
}
// jetzt ist man bei einem leeren Knoten angekommen
bt.setObject(pItem);
return;
}
Löschen (remove)
Die Klasse BinarySearchTree bietet neben der Methode insert auch die Methode remove, mit der man ein Element aus einem Suchbaum löschen kann - und die Suchbaumstruktur bleibt gewahrt!
Das ist sehr angenehm, denn das Löschen von Elementen aus einem Suchbaum ist eine SEHR mühsame Angelegenheit, weil man genau darauf achten muss, dass die Suchbaum-Struktur nicht zerstört wird.
Im folgenden wird dargestellt, wie das Löschen von Elementen aus einem Binären Suchbaum funktioniert.
Implementierung einer Löschmethode
Diese Methode ist nicht relevant für das Zentralabitur!
Das Löschen von Knoten aus binären Suchbäumen ist insofern nicht ganz einfach, als man darauf achten muss, dass die Struktur des binären Suchbaums nicht zerstört wird.
Strategie
Standardfall
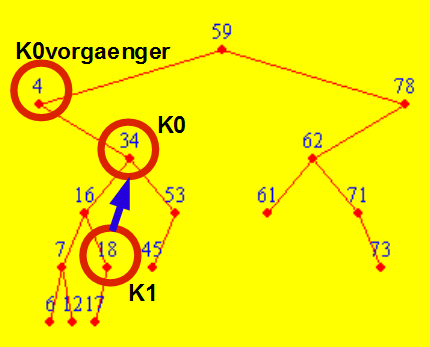
- Den richtigen Knoten suchen: K0. Außerdem braucht man den Vorgänger von K0
- Suche im linken Teilbaum von K0 den Knoten, der am weitesten rechts ist: K1. Außerdem braucht man den Vorgänger von K1
- Hänge den (linken!) Nachfolger von K1 an den Vorgänger von K1.
- K1 ersetzt jetzt K0, d.h. der Inhalt von K1 wird jetzt in den Knoten K0 geschrieben.
Ausnahmefälle
- K0 ist ein Blatt → einfach löschen.
- Die Wurzel des Gesamtbaumes enthält das zu löschende Element
- TODO
- K0 hat keinen linken Teilbaum → Der Nachfolger von K0 ersetzt K0, d.h.:
- Im Vorgänger von K0 wird der Nachfolger von K0 als (richtigen!) Nachfolger eingetragen.
benötigte Methoden
public boolean istBlatt(BinaryTree pTree)public BinaryTree findeK0Vorgaenger(BinaryTree pTree, Object pObject)public BinaryTree findeK1Vorgaenger(BinaryTree pTree)
Implemtierung
public void loeschen(BinaryTree b, String zahl) {
if(b.isEmpty())
{
return;
}
// wenn das zu loeschende Element die Wurzel ist:
// 1. an einen Vater-Knoten anhaengen
// 2. loeschen
// 3. vaterknoten wieder wegnehmen
if(b.getObject().equals(zahl)){
BinaryTree vater = new BinaryTree("-999999");
vater.setRightTree(b);
loeschen(vater, zahl);
b = vater.getRightTree();
return;
}
BinaryTree K0vorgaenger = this.findeVorgaengerKnoten(b,zahl );
System.out.println("Vorgänger von K0:" + K0vorgaenger.getObject());
boolean K0haengtLinksAmVorgaenger = true;
BinaryTree K0 = K0vorgaenger.getLeftTree();
if(!K0vorgaenger.getRightTree().isEmpty() &&
zahl.equals(K0vorgaenger.getRightTree().getObject()))
{
K0 = K0vorgaenger.getRightTree();
K0haengtLinksAmVorgaenger = false;
}
String K0String = (String) K0.getObject();
System.out.println("K0String: "+K0String);
if(istBlatt(K0)){
System.out.println("istBlatt!");
if(K0haengtLinksAmVorgaenger){
K0vorgaenger.setLeftTree(new BinaryTree());
}
else{
K0vorgaenger.setRightTree(new BinaryTree());
}
return;
}
if(K0.getLeftTree().isEmpty()){
K0.setObject(K0.getRightTree().getObject());
K0.setLeftTree(K0.getRightTree().getLeftTree());
K0.setRightTree(K0.getRightTree().getRightTree());
return;
}
BinaryTree K1vorgaenger = vorgaengerVonAmWeitestenRechts(K0.getLeftTree());
System.out.println("K1vorgaenger: " + K1vorgaenger.getObject());
BinaryTree K1 = K1vorgaenger.getRightTree();
System.out.println("K1: " + K1.getObject());
K1vorgaenger.setRightTree(K1.getLeftTree());
K0.setObject(K1.getObject());
return;
}
private boolean istBlatt(BinaryTree pTree) {
boolean ergebnis = pTree.getLeftTree().isEmpty() && pTree.getRightTree().isEmpty();
System.out.println("istBlatt("+pTree.getObject()+"): "+ergebnis);
return ergebnis;
}
private BinaryTree vorgaengerVonAmWeitestenRechts(BinaryTree pTree) {
System.out.println("vorgaengervonAmWeitestenRechts("+pTree.getObject()+")");
if(pTree.getRightTree().isEmpty()){
System.err.println("Fehler in vorgaengerVonAmWeitestenRechts");
return null;
}
if(pTree.getRightTree().getRightTree().isEmpty()){
return pTree;
}
BinaryTree ergebnis = this.vorgaengerVonAmWeitestenRechts(pTree.getRightTree());
return ergebnis;
}
private BinaryTree findeVorgaengerKnoten(BinaryTree pTree, String zahl)
{
System.out.println("findeVorgaengerKnoten("+pTree.getObject()+", "+zahl+")");
if(zahl.equals(pTree.getObject())){
System.err.println(zahl+"ist die Wurzel von pTree selber!!!");
return null;
}
boolean gefunden = false;
int zahl1 = Integer.parseInt(zahl);
BinaryTree ergebnis = pTree;
while(gefunden == false){
String wurzelString = (String) ergebnis.getObject();
int wurzelInt = Integer.parseInt(wurzelString);
System.out.println("wurzelInt" + wurzelInt);
System.out.println("zahl" + zahl);
System.out.println("ergebnis.getObject(): " + ergebnis.getObject());
if(zahl.equals(ergebnis.getRightTree().getObject()) ||
zahl.equals(ergebnis.getLeftTree().getObject()))
{
gefunden = true;
}
else
{
if(zahl1 < wurzelInt){
ergebnis = ergebnis.getLeftTree();
}
else{
ergebnis = ergebnis.getRightTree();
}
}
}
return ergebnis;
}