Graph

Graph für die Distanzen zwischen Städten

Ein Graph ist in der Graphentheorie eine Struktur, die eine Menge von Objekten zusammen mit den zwischen diesen Objekten bestehenden Verbindungen repräsentiert.

Die mathematischen Abstraktionen der Objekte werden dabei Knoten des Graphen genannt. Die paarweisen Verbindungen zwischen Knoten heißen Kanten.

Ein Graph kann entweder als Graph, als Adjazenzliste oder als Adjazenzmatrix dargestellt werden.

Schnittstellenbeschreibung

• Datei:Graph.pdf
• Datei:GraphNode.pdf

TODO: Erklärungen zur Schnittstelle

Adjazenzmatrix

Knoten und Kanten eines Graphen können in Form einer Matrix dargestellt werden. Die Matrix ist dabei spiegelsymmetrisch.

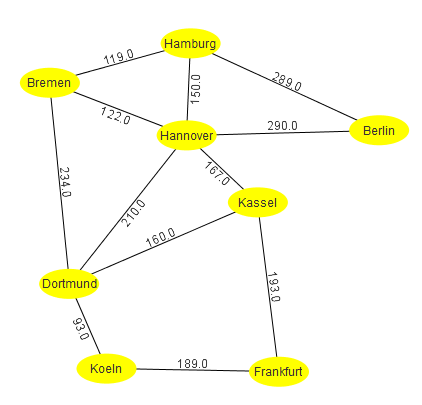
Der oben dargestellte Graph hat folgende Adjazenzmatrix:

	Berlin	Bremen	Dortmund	Frankfurt	Hamburg	Hannover	Kassel	Koeln
Berlin					289	290
Bremen			234		119	122
Dortmund		234				210	160	93
Frankfurt							193	189
Hamburg	289	119				150
Hannover	290	122	210		150		167
Kassel			160	193		167
Koeln			93	189

Traversierungen von Graphen

Wie bei Bäumen gibt es auch bei Graphen viele Anwendungen, in denen ein Graph knotenweise durchlaufen werden muss. Die Traversierungsverfahren ähneln denen bei Bäumen, berücksichtigen allerdings noch die speziellen Gegebenheiten von Graphen, nämlich:

• Graphenknoten können mehr als zwei Nachbarn haben
• Graphen können Querverbindungen und "Kreise" enthalten

Tiefendurchlauf

Erläuterung

Beim Tiefendurchlauf (engl. Depth First Search - DFS) durch einen Baum nimmt man ausgehend von einem Startknoten den ersten Nachbarknoten. Von diesem nimmt man wieder den ersten Nachbarknoten usw. Wenn man dann in eine Sackgasse gerät, geht man eine Stufe zurück und nimmt den nächsten Nachbarknoten. Natürlich werden Knoten, die man schon besucht hat, nicht noch einmal berücksichtigt.

Der Tiefendurchlauf entspricht der Preorder-Traversierung eines Baumes.

Beispiel:

Es gibt für jeden Startknoten mehrere mögliche Tiefendurchläufe, denn man kann sich bei den Nachbarknoten frei entscheiden, welchen man zuerst nimmt. In diesem Beispiel werden die Nachbarknoten immer nach alphabetischer Ordnung genommen.

Tiefendurchlauf für den Startknoten Frankfurt:

Zu Anfang kann man immer direkt weitergehen:

Frankfurt -> Kassel -> Dortmund -> Bremen -> Hamburg -> Berlin -> Hannover

Von Hannover aus ist kein freier Knoten mehr erreichbar. Deswegen muss man jetzt in der Liste zurckgehen, bis man zu einem Knoten kommt, der noch einen freien Nachbarknoten hat. Das ist in diesem Fall Dortmund (der freie Nachbarknoten ist Koeln). Das heißt, Koeln wird als nächstes angehängt, und man würde von Köln aus weitersuchen (wenn es noch freie Knoten gäbe...)

Ergebnis:

Frankfurt -> Kassel -> Dortmund -> Bremen -> Hamburg -> Berlin -> Hannover -> Koeln

Implementierung

Der Tiefendurchlauf durch einen Graphen wird am einfachsten rekursiv programmiert.

 public List tiefendurchlauf(Graph pGraph, GraphNode pNode){
   List knoten = new List();
   knoten.append(pNode);
   pNode.mark();
   //Alle Nachbarn des Startknoten holen
   List nachbarnListe = pGraph.getNeighbours(pNode);
   //Nachbarn mit while-Schleife durchlaufen
   nachbarnListe.toFirst();
   while(nachbarnListe.hasAccess()){
     GraphNode aktuellerNachbar = (GraphNode)h.getObject();
     //Wenn der aktuelle Nachbar nicht markiert ist, also noch nicht besucht wurde,
     //zur Liste hinzufuegen und auch seine Nachbarn durch den rekursiven Aufruf besuchen.
     if( !aktuellerNachbar.isMarked() ){
       //Rekursiver Aufruf
       List weitereKnotenListe = tiefendurchlauf(pGraph, aktuellerNachbar);
       knoten.concat(weitereKnotenListe);
     }
     nachbarnListe.next();
   }
   return knoten;
 }

Breitendurchlauf

Der Breitendurchlauf (engl. breadth first search - BFS) ist eine Methode, um alle Knoten eines Graphen aufzuzählen.

Erläuterung

Mit dem Breitendurchlauf werden die Knoten in folgender Reihenfolge aufgezählt:

1. zuerst der Startknoten,
2. dann die Nachbarknoten des Startknotens, d.h. alle Knoten, die vom Startknoten aus über eine Kante erreichbar sind.
3. dann die Knoten, die vom Startknoten aus mit zwei Kanten erreichbar sind.
4. usw.

Knoten, die schon einmal aufgezählt wurden, werden natürlich nicht wieder aufgezählt.

Im Binärbaum ist der Breitendurchlauf genau Levelorder.

Beispiel

Beim Breitendurchlauf gibt es für jeden Startknoten mehrere Möglichkeiten, denn mann kann zwischen den Nachbarknoten wählen. Hier werden die Nachbarknoten immer in alphabetischer Reihenfolge betrachtet.

Breitendurchlauf für den Startknoten Frankfurt

Erst der Startknoten und seine Nachbarknoten:

Frankfurt -> Kassel -> Koeln

Jetzt wird von den Nachbarknoten der erste genommen und dessen Nachbarknoten werden betrachtet:

Frankfurt -> Kassel -> Koeln -> Dortmund -> Hannover

Der nächste Knoten in der Liste, der noch freie Nachbarknoten hat, ist Dortmund:

Frankfurt -> Kassel -> Koeln -> Dortmund -> Hannover -> Bremen

Schließlich die Nachbarknoten von Hannover:

Frankfurt -> Kassel -> Koeln -> Dortmund -> Hannover -> Bremen -> Berlin -> Hamburg

Beim Breitendurchlauf wird also zuerst die "nähere Umgebung" betrachtet.

Implementierung

Die Implementierung setzt darauf auf, dass der Graph linearisiert wird:

Man braucht eine knotenListe; in diese werden nach und nach alle Knoten des Graphen gemäß der Breitendurchlauf-Reihenfolge eingefügt.

1. zuerst wird der Startknoten als besucht markiert und in knotenListe eingefügt.
2. Dann wird knotenListe von Anfang bis Ende durchlaufen. Dabei passiert folgendes:
   1. Für jeden Nachbarknoten des aktuellen Knoten wird überprüft, ob er schon besucht wurde. Wenn nein, dann wird er als besucht markiert und in knotenListe eingefügt.

So wächst die knotenListe von einem Element (=dem Startknoten) beginnend immer weiter an, während sie durchlaufen wird. Die Schleife kommt zum Ende, wenn alle Knoten eingefügt und als besucht gekennzeichnet sind.

  public List breitenDurchlauf(Graph pGraph, GraphNode startKnoten){
     List knotenListe = new List();
     startKnoten.mark();
     knotenListe.append(startKnoten);
     knotenListe.toFirst();
     while(knotenListe.hasAccess()){
        GraphNode aktuell = (GraphNode) knotenListe.getObject();
        List nachbarn = pGraph.getNeighbours(aktuell);
        nachbarn.toFirst();
        while(nachbarn.hasAccess()){
           GraphNode aktuellerNachbar = (GraphNode)nachbarn.getObject();
           if(!aktuellerNachbar.isMarked()){
              aktuellerNachbar.mark();
              knotenListe.append(aktuellerNachbar);
           }
           nachbarn.next();
        }
        knotenListe.next();
     }
     return knotenListe;
  }

Kürzeste Wege in Graphen: Der Dijkstra-Algorithmus

Mit Hilfe des Dijkstra-Algorithmus kann man für einen Startknoten die kürzesten Wege zu allen anderen Knoten des Graphen bestimmen.

Idee des Dijkstra-Algorithmus

Notwendige Datenstrukturen

• Für jeden Knoten wird der Vorgänger und ein Wert distanz gespeichert; distanz gibt die bisher beste gefundene Distanz zum Startknoten an.
• gelbe Liste: In dieser Liste werden Knoten gespeichert, für die schon ein Distanzwert vorliegt, deren Distanz zum Startknoten aber noch nicht abschließend festgelegt werden konnte. Die Knoten erscheinen in der gelben Liste gemäß ihrem Distanzwert, und zwar in aufsteigender Reihenfolge.
• rote Liste: Man braucht eine Liste, in der alle Knoten gespeichert werden, deren Distanz zum Startknoten abschließend festgestellt wurde.

Algorithmus

1. Die Distanz des Startknoten wird auf 0 gesetzt; der von allen anderen Knoten auf unendlich.
2. Der Startknoten wird in die rote Liste eingefügt.
3. Alle Nachbarknoten des Startknotens werden in die gelbe Liste eingefügt, und zwar gemäß ihrer Distanz zum Startknoten.
4. Die folgenden Schritte laufen jetzt so lange, bis die gelbe Liste leer ist:
   1. den ersten Knoten aus der gelben Liste (im folgenden ersterGelber) entnehmen und in die rote Liste einfügen. Denn die Distanz dieses Knotens ist endgültig geklärt.
   2. für alle Nachbarknoten von ersterGelber überprüft man:
      1. wenn sie noch nicht in der gelben Liste sind: Distanz berechnen (=Distanz von ersterGelber plus Kantenlänge von ersterGelber) und dann in die gelbe Liste hinzufügen (=gemäß der Distanz einfügen)
      2. wenn sie schon in der gelben Liste sind: Überprüfen, ob die Distanz von ersterGelber plus Kantenlänge kleiner ist als die bisher gespeicherte Distanz: Dann hat man eine bessere Route gefunden! Die Distanz des Nachbarknoten wird dann entsprechend verbessert, wodurch sich seine Position in der gelben Liste verbessert.

Kürzester Weg für einen beliebigen Knoten Die Distanz kann man direkt aus dem Knoten auslesen.

Den kürzesten Weg von einem beliebigen Knoten zum Startknoten kann man jetzt angeben, indem man sich von dem Knoten aus immer zum nächsten Vorgänger hangelt, bis mn schließlich beim Startknoten angekommen ist.

Beispiel

Für den Startknoten Frankfurt sind die ersten Schritte des Dijkstra-Algorithmus die folgenden. Dabei wird in Klammern immer die aktuelle Distanz angegeben und der Vorgängerknoten (als Nummernschild) angegeben.

• Frankfurt (0, --), alle anderen Knoten (unendlich)
• Schritt 1: Frankfurt
  • rote Liste: Frankfurt (0, --)
  • gelbe Liste: Koeln (189, F), Kassel (193, F)
• Schritt 2: Koeln
  • rote Liste: Frankfurt (0, --), Koeln (189, F)
  • gelbe Liste: Kassel (193, F), Dortmund (189+93=282, K)
• Schritt 3: Kassel
  • rote Liste: Frankfurt (0, --), Koeln (189, F), Kassel (193, F)
  • gelbe Liste: Dortmund (282, K), Hannover(193+167=360, KS)
• Schritt 4: Dortmund
  • rote Liste: Frankfurt (0, --), Koeln (189, F), Kassel (193, F), Dortmund (282, K)
  • gelbe Liste: Hannover (360, KS), Bremen (282+234=516, DO)
  • Hannover ist auch von Dortmund aus erreichbar, aber die bisherige Distanz über Kassel ist geringer!
• Schritt 5: Hannover
  • rote Liste: Frankfurt (0, --), Koeln (189, F), Kassel (193, F), Dortmund (282, K), Hannover (360, KS)
  • gelbe Liste: Hamburg (510, H), Bremen (360+122=482, H), Berlin (360+290=650, H)
  • Hamburg kam neu dazu und setzt sich an die Spitze der gelben Liste.
  • Bremen ist über Hannover schneller erreichbar als bisher über Dortmund, deswegen wurde Bremen geupdated.

//TODO Die weiteren Schritte darstellen.

Implementierung

Diese Implementierung umfasst zwei Klassen:

• DijkstraAlgorithmus
• DijkstraNode

Die Klasse DijkstraAlgorithmus enthält eine (lange...) Methode initMap, damit man das Ganze auch testen kann.

Klasse DijkstraAlgorithmus:

import listen.List;
import listen.ListWithViewer;

public class DijkstraAlgorithmus {
  GraphWithViewer map;
  ListWithViewer gelbeListe;
  
  
  public void initMap(){
     map = new GraphWithViewer();
     DijkstraGraphNode kiel = new DijkstraGraphNode("Kiel");
     map.addNode(kiel);
     DijkstraGraphNode luebeck = new DijkstraGraphNode("Luebeck");
     map.addNode(luebeck);
     DijkstraGraphNode hamburg = new DijkstraGraphNode("Hamburg");
     map.addNode(hamburg);
     DijkstraGraphNode berlin = new DijkstraGraphNode("Berlin");
     map.addNode(berlin);
     DijkstraGraphNode bremen = new DijkstraGraphNode("Bremen");
     map.addNode(bremen);
     DijkstraGraphNode hannover = new DijkstraGraphNode("Hannover");
     map.addNode(hannover);
     DijkstraGraphNode dortmund = new DijkstraGraphNode("Dortmund");
     map.addNode(dortmund);
     DijkstraGraphNode bochum = new DijkstraGraphNode("Bochum");
     map.addNode(bochum);
     DijkstraGraphNode koeln = new DijkstraGraphNode("Koeln");
     map.addNode(koeln);
     DijkstraGraphNode bonn = new DijkstraGraphNode("Bonn");
     map.addNode(bonn);
     DijkstraGraphNode mainz = new DijkstraGraphNode("Mainz");
     map.addNode(mainz);
     DijkstraGraphNode frankfurt = new DijkstraGraphNode("Frankfurt");
     map.addNode(frankfurt);
     DijkstraGraphNode kassel = new DijkstraGraphNode("Kassel");
     map.addNode(kassel);
     DijkstraGraphNode wuerzburg = new DijkstraGraphNode("Wuerzburg");
     map.addNode(wuerzburg);
     DijkstraGraphNode leipzig = new DijkstraGraphNode("Leipzig");
     map.addNode(leipzig);
     DijkstraGraphNode nuernberg = new DijkstraGraphNode("Nuernberg");
     map.addNode(nuernberg);
     DijkstraGraphNode stuttgart = new DijkstraGraphNode("Stuttgart");
     map.addNode(stuttgart);
     DijkstraGraphNode muenchen = new DijkstraGraphNode("Muenchen");
     map.addNode(muenchen);
     DijkstraGraphNode karlsruhe = new DijkstraGraphNode("Karlsruhe");
     map.addNode(karlsruhe);

     map.addEdge(kiel, hamburg, 97);
     map.addEdge(kiel, luebeck, 84);
     map.addEdge(luebeck, hamburg, 74);
     map.addEdge(luebeck, berlin, 284);
     map.addEdge(berlin, hamburg, 289);
     map.addEdge(hamburg, bremen, 119);
     map.addEdge(bremen, hannover, 122);
     map.addEdge(hannover, hamburg, 150);
     map.addEdge(berlin, hannover, 290);
     map.addEdge(berlin, leipzig, 188);
     map.addEdge(hannover, kassel, 167);
     map.addEdge(leipzig, kassel, 250);
     map.addEdge(kassel, dortmund, 160);
     map.addEdge(dortmund, bremen, 234);
     map.addEdge(dortmund, hannover, 210);
     map.addEdge(dortmund, bochum, 22);
     map.addEdge(dortmund, koeln, 93);
     map.addEdge(koeln, bochum, 82);
     map.addEdge(koeln, bonn, 29);
     map.addEdge(bonn, mainz, 169);
     map.addEdge(frankfurt, mainz, 45);
     map.addEdge(frankfurt, kassel, 193);
     map.addEdge(leipzig, nuernberg, 278);
     map.addEdge(kassel, wuerzburg, 209);
     map.addEdge(wuerzburg, nuernberg, 110);
     map.addEdge(wuerzburg, frankfurt, 119);
     map.addEdge(nuernberg, muenchen, 166);
     map.addEdge(muenchen, stuttgart, 223);
     map.addEdge(nuernberg, stuttgart, 208);
     map.addEdge(stuttgart, karlsruhe, 82);
     map.addEdge(karlsruhe, frankfurt, 147);
     map.addEdge(frankfurt, koeln, 189);
     map.switchToISOMLayout();
  }
  
  public void dijkstraAlgorithmus(String startpunkt) {
     gelbeListe = new ListWithViewer();
     DijkstraGraphNode startNode = (DijkstraGraphNode) map.getNode(startpunkt);
     startNode.setDistanz(0);
     gelbeListe.append(startNode);
     while(gelbeListe.isEmpty() == false){
        gelbeListe.toFirst();
        DijkstraGraphNode node = (DijkstraGraphNode) gelbeListe.getObject();
        //System.out.println("node: "+node);
        gelbeListe.remove();
        node.mark();
        node.ausgeben();
        List neighbours = map.getNeighbours(node);
        neighbours.toFirst();
        while(neighbours.hasAccess()){
           DijkstraGraphNode currentNeighbour = (DijkstraGraphNode) neighbours.getObject();
           //System.out.println("currentNeighbour: "+currentNeighbour);
           double streckeNodeCurrentNeighbour = map.getEdgeWeight(node, currentNeighbour);
           if(currentNeighbour.getDistanz() > node.getDistanz()+streckeNodeCurrentNeighbour){
              // ueber node fuehrt eine kuerzere Strecke zu currentNeighbour!
              currentNeighbour.setVorgaenger(node);
              currentNeighbour.setDistanz(node.getDistanz()+streckeNodeCurrentNeighbour);
              // currentNeighbour in gelbeListe einfuegen bzw. ersetzen
              inGelbeListeUpdaten(currentNeighbour);
           }
           neighbours.next();
        }
     }
  }

  /**
   * sorgt dafuer, dass node gemaess seiner Distanz 
   * die richtige Position in der gelbeListe bekommt.
   * wenn node noch gar nicht in gelbeListe enthalten ist, 
   * dann wird node an der richtigen Stelle eingefuegt. 
   */
  private void inGelbeListeUpdaten(DijkstraGraphNode node) {
     boolean inserted = false;
     gelbeListe.toFirst();
     while(gelbeListe.hasAccess()){
        DijkstraGraphNode aktuell = (DijkstraGraphNode) gelbeListe.getObject();
        if(aktuell.getDistanz() >= node.getDistanz()){
           gelbeListe.insert(node);
           inserted = true;
           break;
        }
        gelbeListe.next();
     }
     if(inserted){
        // ggf. taucht currentNeighbour nochmal in der Liste auf!
        // dann muss er entfernt werden!
        while(gelbeListe.hasAccess()){
           DijkstraGraphNode aktuell = (DijkstraGraphNode) gelbeListe.getObject();
           if(aktuell.getName().equals(node.getName())){
              gelbeListe.remove();
              break;
           }
           gelbeListe.next();
        }
     }
     else{
        // der Knoten wurde noch nicht eingefuegt!
        gelbeListe.append(node);
     }
     
  }
  
  public static void main(String[] args) {
     DijkstraAlgorithmus da = new DijkstraAlgorithmus();
     da.initMap();
     da.dijkstraAlgorithmus("Muenchen");
  }
}

Klasse DijktstraGraphNode:

import listen.List;

public class DijkstraGraphNode extends GraphNode implements Comparable {
  
  // es werden der Vorgaenger und die (bisher beste) Distanz zum Startknoten gespeichert.
  private DijkstraGraphNode vorgaenger;
  private double distanz;
  
  public DijkstraGraphNode(String name) {
     super(name);
     distanz = 1000000;
  }
  
  public void setDistanz(double distanz){
     this.distanz = distanz;
  }
  
  public double getDistanz(){
     return distanz;
  }
  
  public void setVorgaenger(DijkstraGraphNode pNode){
     this.vorgaenger = pNode;
  }
  
  private DijkstraGraphNode getVorgaenger() {
     return vorgaenger;
  }

  public void ausgeben(){
     DijkstraGraphNode aktuell = this;
     while(aktuell != null){
        System.out.print(aktuell+"<-");
        aktuell = aktuell.getVorgaenger();
     }
     System.out.println();
  }
  
  public String toString(){
     String ergebnis = this.getName()+": "+this.distanz;
     return ergebnis;
  }

  /**
   * vergleicht zwei DijkstraGraphNodes gemaess ihrer Distanz.
   * diese Methode sorgt fuer die Implementierung der Schnittstelle Comparable;
   * damit koennen dann z.B. Vectoren mit Inhalt DijkstraGraphNode einfach sortiert werden.
   */
  public int compareTo(Object arg0) {
     DijkstraGraphNode dgn2 = (DijkstraGraphNode) arg0;
     if(this.distanz < dgn2.distanz){
        return -1;
     }
     if(this.distanz > dgn2.distanz){
        return 1;
     }
     return 0;
  }

}

Anwendungsbeispiele zu Graphen

Minimaler Spannbaum

Ein Minimaler Spannbaum besteht aus einer Liste von Kanten des Graphen, die folgenden Bedingungen genügen muss:

1. die Kanten der Liste müssen alle Knoten des Graphen miteinander verbinden.
2. die Gesamtlänge der Kanten in der Liste muss (im Hinblick auf die Erfüllung der 1. Bedingung) minimal sein.

Beispiel aus der Praxis

Eine Stromfirma will ein Leitungsnetz aufbauen, das alle Städte verbindet. Keine Stadt darf ausgelassen werden. Das Stromnetz soll aber möglichst kurz sein.

Implementierung

1. Zu Anfang erzeugt man einen ergebnisgraph, der nur die Knoten des ursprünglichen Graphen enthält, aber nicht die Kanten.
2. Alle Kanten des gesamten ursprünglichen Graphen werden ausgelesen werden ihrem Gewicht nach durchgegangen, wobei man beim kleinsten Gewicht anfängt.
   1. Kann die momentan betrachtete Kante in den ergebnisgraph eingefuegt werden, ohne dass ein Kreis entsteht, wird sie eingefügt.

Hauptmethode

 public Graph minimalerSpannbaum(Graph pGraph){
    //es wird ein neuer Graph erstellt, der das Ergebnis hinterher anzeigt
    Graph ergebnisGraph = new Graph();
    //alle Knoten des uebergebenen Graphen werden in den spaeteren Ergebnisgraphen eingetragen
    List nnodes = pGraph.getNodes();
    nnodes.toFirst();
    while(nnodes.hasAccess()){
       GraphNode akt = (GraphNode)nnodes.getObject();
       ergebnis.addNode(akt);
       nnodes.next();
    }
    //alle Kanten werden ihrem Gewicht nach sortiert in einem Vector uebergeben
    Vector<Edge> edges = alleKantenSortiert(pGraph);
    //dieser Vector wird duchgegangen
    for(int i = 0; i < edges.size(); i++){
    //kann die aktuell im Vector betrachtete Kante eingefuegt werden, ohne dass ein Kreis entsteht,
    //wird sie eingefuegt   
    Edge akt = edges.elementAt(i);
       if(!erzeugtKreis(ergebnisGraph, edges.elementAt(i))){
          ergebnisGraph.addEdge(akt.getNodeA(), akt.getNodeB(), akt.getWeight());
          System.out.println("addEdge");
       }
    }
    return ergebnisGraph;
 }

Hilfsmethoden

Fuer die Ueberpruefung ob ein Kreis erzeugt wird ist eine eigene Methode hilfreich. Hier wird von einem Knoten der einzufuegenden Kantre ausgehend ueberprueft, ob der andere Knoten erreichbar ist. Wenn ja, dann wuerde durch einfuegen ein Kreis erzeugt, wenn nein nicht.

 private boolean erzeugtKreis(Graph pGraph, Edge pEdge) {
    //von dem einen Knoten aus erreichbare Nodes werden ausgelesen un in einer Liste gespeichert
    List erreichbare = erreichbareNodes(pGraph, pEdge.getNodeA());
    //und werden durchgegangen
    erreichbare.toFirst();
    while(erreichbare.hasAccess()){
       //wird der Knoten, von dem ausgegangen wurde gefunden wuerde ein Kreis erzeugt und true ausgegeben
       if(pEdge.getNodeB() == (GraphNode)erreichbare.getObject()){
          return true;
       }
       erreichbare.next();	
    }
    //wird der KNoten nicht gefunden wird false zurueckgegeben, da kein Kreis erzeugt wuerde
    return false;
 }

Anmerkung: Es gibt natürlich noch weitere Möglichkeiten die Strategie zu realisieren. Eine sehr einfache kommt ohne die Methode erreichbareNodes(...) aus: Man markiert alle bereits verbundenen Knoten (im Bsp. eines Stromnetzes: alle bereits "angeschlossenen" Knoten), also beim Einfügen jeder Kante die zu ihr gehörenden Knoten, falls diese noch nicht markiert sind. Diese Taktik macht das Überprüfen, ob beim Einfügen ein Kreis entsteht, sehr einfach: Falls beide zur Kante gehörenden Knoten bereits markiert sind, entstünde ein Kreis und die Kante darf nicht eingefügt werden.

Erreichbare Knoten

Um alle erreichbaren Knoten zu bekommen erstellen wir erst eine Liste ergebnis, die am Ende ausgegen wird.Danach wird der Liste ergebnis der startNode angehangen. Dieses Node wird dann im Graphen makiert. Danach wird eine while-Schleife geöffnet, die solange läuft wie die Liste ergebnis ein aktuelles Objekt besitzt. Sie fügt die Nachbarn des aktuellen Nodes in eine Liste nachbarliste1 ein. Eine weitere while-Schleife wird geöffnet, die solange läuft, wie die Liste nachbarliste1 ein aktuelles Objekt hat. Wenn das aktuelle Node nicht markiert ist wird das Objekt dem ergebnis angefügt (also der erreichbare Nachbar wird in das Ergebnis geschrieben) und das Node wird makiert. So werden am Ende mit der Liste ergebnis alle erreichbare Nachbarn ausgegeben.

public List erreichbareNodes(Graph pGraph,GraphNode pNode){
 pGraph.resetMarks();
 List ergebnis = new List();
 ergebnis.append(pNode);
 pNode.mark();
 ergebnis.toFirst();
 while(ergebnis.hasAccess()){
   GraphNode akt1=(GraphNode) ergebnis.getObject();
   List nachbarliste1 =pGraph.getNeighbours(akt1);
   nachbarliste1.toFirst();
   while(nachbarliste1.hasAccess()){
     GraphNode akt2=(GraphNode) nachbarliste1.getObject();
     if(akt2.isMarked()==false){
       ergebnis.append(akt2);
       akt2.mark();
     }
   nachbarliste1.next();
   }
   ergebnis.next();
 }
 return ergebnis;
}

Beispiel: Knoten mit ungerader Kantenzahl markieren

TODO: Methode erklären

 TODO: Quelltext gut kommentiert einfügen

Beispiel: Summe der Kantenkosten eines Knotens bestimmen

 public int Kantenkosten(GraphWithViewer pGraph, GraphNode pNode)
 {
 int ergebnis = 0;   // Variable zum Speichern der Kosten wird deklariert
 List nachbarn = pGraph.getNeighbours(pNode);
 nachbarn.toFirst();
 while(nachbarn.hasAccess()) // Schleife durchläuft einmal alle Nachbarn
 {
  GraphNode akt = (GraphNode)nachbarn.getObject();
  int help = (int) pGraph.getEdgeWeight(pNode, akt);
  ergebnis=ergebnis+help; //Distanz wird hinzugefügt
  nachbarn.next();
 }
 return ergebnis; // Distanz wird ausgegeben
 }

Beispiel: Knoten mit maximalen Kantenkosten bestimmen

TODO: Methode erklären

 TODO: Quelltext gut kommentiert einfügen

Beispiel: Nächsten Nachbarn eines Knotens bestimmen

Strategie:

Man entfernt alle markierten Nodes aus der NachbarListe und durchläuft diese Liste und guckt, welches die kürzeste Kante zu pNode hat.

  public GraphNode gibNaechstenNachbarn(GraphWithViewer gwv, GraphNode pNode)
  {
     GraphNode ergebnis = null;
     double gewicht;
     List nachbarListe = gwv.getNeighbours(pNode);
     //  alle Nachbarn werden in die NachbarListe eingefügt
     nachbarListe.toFirst();
        while(nachbarListe.hasAccess())
        {
        GraphNode aktKn=(GraphNode)nachbarListe.getObject();
        if(aktKn.isMarked())
        //  wenn ein Objekt der NachbarListe markiert ist, dann wird es entfernt.
        {
        nachbarListe.remove();
        }
        else{
           nachbarListe.next();
       }
     }
     nachbarListe.toFirst();
     // das erste Objekt der nachbarListe wird als Ergebnis deklariert
     // und das Gewicht der Kante von diesem Objekt zu pNode als Gewicht
     ergebnis = (GraphNode)nachbarListe.getObject();
     gewicht = gwv.getEdgeWeight(pNode, ergebnis);
     nachbarListe.next();
     while(nachbarListe.hasAccess())
     {
        GraphNode aktuellerNode = (GraphNode)nachbarListe.getObject();
        double aktuellesGewicht = gwv.getEdgeWeight(pNode, aktuellerNode);
        if(aktuellesGewicht<gewicht)
        // wenn ein Gewicht einer Kante von einem Nachbarn zu pNode kleiner ist als das Gewicht,
        // dann wird dieses das neue Gewicht und der Nachbar wird das Ergebnis
        {
           ergebnis = aktuellerNode;
           gewicht = gwv.getEdgeWeight(pNode, aktuellerNode);
        }		
        nachbarListe.next();
     }
     return ergebnis;
  }

Beispiel: Überprüfen, ob im Graphen ein Dreierkreis existiert

TODO: Methode erklären

 TODO: Quelltext gut kommentiert einfügen

Beispiel: Alle Nachbarn zählen

TODO: Quellcode erklären und im Quellcode kommentieren

  public int zaehleNachbarn(GraphWithViewer pGraph, GraphNode pNode){
    int ergebnis = 0;
    List neighbours = graph.getNeighbours(pNode);
 
    neighbours.toFirst();
    while(neighbours.hasAccess()){
       ergebnis++;
       neighbours.next();
    }
    return ergebnis;
  } 

Beispiel: Wer hat die meisten Nachbarn

TODO: Quellcode erklären und im Quellcode kommentieren

   public String meisteNachbarn(GraphWithViewer Ggraph){
       List hilfe=new List();
       hilfe.concat(Ggraph.getNodes());
       hilfe.toFirst();
       GraphNode aktNode =null;
       int max=-1;
       while(hilfe.hasAccess())
       {
           GraphNode aktuell=(GraphNode)hilfe.getObject();
           int akt=this.kantenzahl(Ggraph, aktuell);
           if(akt>max)
           {
               max=akt;
               aktNode=(GraphNode)hilfe.getObject();
           }
           else{
               hilfe.next();
           }
       }
       System.out.println(max);
       return aktNode.getName();
   }