Deterministischer Endlicher Automat
Ein deterministischer endlicher Automat erhält ein Wort als Eingabe und akzeptiert dieses Wort oder nicht.
Die Menge der akzeptierten Wörter bildet die durch den deterministischen endlichen Automaten dargestellte Sprache.
Sprachen, die von deterministischen endlichen Automaten akzeptiert werden, heißen reguläre Sprache.
Definition
Ein deterministischer, endlicher Automat wird durch ein 5-Tupel (A, Z, d, q0, E) spezifiziert:
- Das Eingabealphabet A ist eine endliche, nicht leere Menge von Symbolen. Buchstaben des Eingabealphabetes werden in der Regel klein geschrieben.
- Z ist eine endliche, nicht leere Menge von Zuständen Z
- d: Z x A → Z ist die Zustandsübergangsfunktion
- q0 ∈ Z ist der Anfangszustand
- E ⊆ Z ist die Menge der Endzustände
Die Zustandsübergangsfunktion kann durch einen Übergangsgraphen oder durch eine Tabelle dargestellt werden.
Beispiel
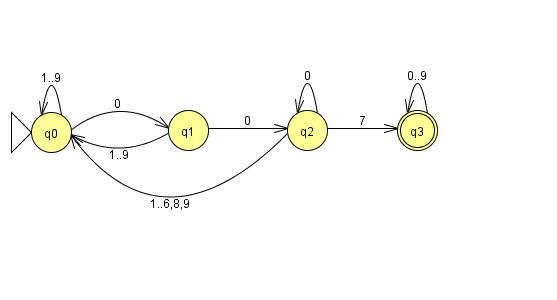
Der 007-Automat:
Zur Sprache gehören all diejenigen Ziffernfolgen, die an beliebiger Stelle die Ziffernfolge "007" enthalten.
- Eingabealphabet: A = {0, 1, ..., 9}
- Zustände: Z = {q0, q1, q2, q3}
- Zustandsübergangsfunktion wird durch den Übergangsgraph rechts dargestellt.
- Anfangszustand: q0 (im Graph: ein Dreieck)
- Endzustände: {q3} (im Graph: ein Doppelkreis)
Die Zustandsübergangsfunktion kann auch als Tabelle dargestellt werden:
| q0 | q1 | q2 | q3 | |
|---|---|---|---|---|
| q0 | 1..9 | 0 | ||
| q1 | 1..9 | 0 | ||
| q2 | 1..6,8,9 | 0 | 7 | |
| q3 | 0..9 |