Backtracking: Unterschied zwischen den Versionen
| (4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
[[Kategorie:Algorithmen]] | [[Kategorie:Algorithmen]] | ||
<font color='red'>'''nur relevant für den Leistungskurs!'''</font> | <font color='red'>'''nur relevant für den Leistungskurs!'''</font> | ||
= Erklärvideos = | |||
* [https://youtu.be/dYwatqXIUkw Rucksackproblem mit Backtracking lösen: Java Implementierung] | |||
= Idee = | = Idee = | ||
''Der folgende Text ist gekürzt aus der Wikipedia [http://de.wikipedia.org/wiki/Backtracking] übernommen. '' | ''Der folgende Text ist gekürzt aus der Wikipedia [http://de.wikipedia.org/wiki/Backtracking] übernommen. '' | ||
| Zeile 13: | Zeile 17: | ||
''Die folgende Beschreibung ist gekürzt und leicht verändert aus der Wikipedia [http://de.wikipedia.org/wiki/Backtracking] übernommen. '' | ''Die folgende Beschreibung ist gekürzt und leicht verändert aus der Wikipedia [http://de.wikipedia.org/wiki/Backtracking] übernommen. '' | ||
<code> | <code> | ||
Teillösung ist zu Anfang leer. | Teillösung ist zu Anfang leer. | ||
Stufe ist 0. | Stufe ist 0. | ||
| Zeile 27: | Zeile 31: | ||
c) rekursiver Aufruf: FindeLoesung(Stufe+1, Teillösung) | c) rekursiver Aufruf: FindeLoesung(Stufe+1, Teillösung) | ||
d) Mache die Erweiterung der Teillösung rückgängig | d) Mache die Erweiterung der Teillösung rückgängig | ||
</code> | </code> | ||
= Backtracking für kürzeste Wege auf Graphen = | = Backtracking für kürzeste Wege auf Graphen = | ||
| Zeile 55: | Zeile 59: | ||
Mithilfe dieser lässt sich der Algorithmus so beschreiben: | Mithilfe dieser lässt sich der Algorithmus so beschreiben: | ||
<code> | <code> | ||
'''findeKuerzestenWegBacktracking (pNode)''' | '''findeKuerzestenWegBacktracking (pNode)''' | ||
'''Abbruchbedingung:''' | '''Abbruchbedingung:''' | ||
| Zeile 71: | Zeile 75: | ||
- aktuelleDistanz wieder zurücksetzen | - aktuelleDistanz wieder zurücksetzen | ||
- die Markierung des Nachbarn entfernen | - die Markierung des Nachbarn entfernen | ||
</code> | </code> | ||
==Implementierung== | ==Implementierung== | ||
| Zeile 82: | Zeile 86: | ||
* die '''rekursive Backtracking-Methode''' <code>kuerzestenWegFindenBacktracking(GraphNode pNode)</code> | * die '''rekursive Backtracking-Methode''' <code>kuerzestenWegFindenBacktracking(GraphNode pNode)</code> | ||
<code> | <code> | ||
'''// Attribute''' | '''// Attribute''' | ||
public GraphWithViewer graph; | public GraphWithViewer graph; | ||
| Zeile 153: | Zeile 157: | ||
return; | return; | ||
} | } | ||
</code> | </code> | ||
=Backtracking für Arrays: Magisches Quadrat= | =Backtracking für Arrays: Magisches Quadrat= | ||
| Zeile 168: | Zeile 172: | ||
* Das eigentliche Backtracking findet in der Methode <u><code>public void findeLoesung(int pStufe)</code></u> statt; diese Methode wird von der Rahmenmethode <code>public void findeLoesung()</code> aufgerufen. | * Das eigentliche Backtracking findet in der Methode <u><code>public void findeLoesung(int pStufe)</code></u> statt; diese Methode wird von der Rahmenmethode <code>public void findeLoesung()</code> aufgerufen. | ||
<code> | <code> | ||
public class MagischesQuadratFertig { | public class MagischesQuadratFertig { | ||
| Zeile 299: | Zeile 303: | ||
} | } | ||
} | } | ||
</code> | </code> | ||
=Aufgabe: Backtracking für Arrays: Rucksackproblem selber programmieren= | =Aufgabe: Backtracking für Arrays: Rucksackproblem selber programmieren= | ||
| Zeile 318: | Zeile 322: | ||
'''Viel Spaß beim Programmieren!''' | '''Viel Spaß beim Programmieren!''' | ||
<code> | <code> | ||
public class Rucksackproblem { | public class Rucksackproblem { | ||
public int[] '''gewichte''' = {28, 57, 33, 18, 99, 42, 17, 52}; | public int[] '''gewichte''' = {28, 57, 33, 18, 99, 42, 17, 52}; | ||
| Zeile 386: | Zeile 390: | ||
} | } | ||
} | } | ||
</code> | </code> | ||
=Aufgabe: Backtracking zum Lösen von Sudokus= | =Aufgabe: Backtracking zum Lösen von Sudokus= | ||
| Zeile 393: | Zeile 397: | ||
Abhilfe schafft hier ein geeignetes Java-Programm! | Abhilfe schafft hier ein geeignetes Java-Programm! | ||
Die "langweiligen" Hilfsmethoden sind unten schon programmiert - es fehlt nur noch die Methode <code>loesenMitBacktracking()</code>. | Die "langweiligen" Hilfsmethoden sind unten schon programmiert - es fehlt nur noch die Methode <code>loesenMitBacktracking(int pStufe)</code>. | ||
<u>Hinweise</u>: | <u>Hinweise</u>: | ||
| Zeile 399: | Zeile 403: | ||
* Die "Teillösung" muss man nicht als Parameter der Backtracking-Methode übergeben, weil immer das Array <code>zahlen</code> entsprechend aktualisiert wird. | * Die "Teillösung" muss man nicht als Parameter der Backtracking-Methode übergeben, weil immer das Array <code>zahlen</code> entsprechend aktualisiert wird. | ||
* Die "Stufe" | * Die "Stufe" beginnt nicht bei 0, sondern bei der Anzahl der belegten Felder. Dann kann der Backtracking-Algorithmus abbrechen, sobald man die Stufe 81 erreicht. | ||
<code> | |||
'''public class Sudoku {''' | |||
<code> | |||
// Das "schwerste Sudoku der Welt" | // Das "schwerste Sudoku der Welt" | ||
// https://www.oe24.at/welt/Das-ist-das-schwierigste-Sudoku-der-Welt/1597831 | // https://www.oe24.at/welt/Das-ist-das-schwierigste-Sudoku-der-Welt/1597831 | ||
| Zeile 419: | Zeile 421: | ||
{0,0,0,0,0,9,7,0,0} | {0,0,0,0,0,9,7,0,0} | ||
}; | }; | ||
'''public static void main(String[] args) {''' | '''public static void main(String[] args) {''' | ||
Sudoku s = new Sudoku(); | Sudoku s = new Sudoku(); | ||
System.out.println("*** Aufgabe ***"); | System.out.println("*** Aufgabe ***"); | ||
s.ausgeben(); | s.ausgeben(); | ||
s.loesenMitBacktracking(); | int belegteFelder = s.belegteFelder(); | ||
boolean erfolg = s.loesenMitBacktracking(belegteFelder); | |||
if(erfolg == true){ | |||
System.out.println("Loesung gefunden!"); | |||
} | |||
else{ | |||
System.out.println("keine Loesung"); | |||
} | |||
} | |||
'''public boolean loesenMitBacktracking(int pStufe){''' | |||
'''//TODO''' | |||
return false; | |||
} | } | ||
| Zeile 472: | Zeile 486: | ||
return true; | return true; | ||
} | } | ||
/** | /** | ||
* ueberprueft, ob das Quadrat ok ist, | * ueberprueft, ob das Quadrat ok ist, | ||
| Zeile 485: | Zeile 499: | ||
int startSpalte = pSpaltenNr - pSpaltenNr%3; | int startSpalte = pSpaltenNr - pSpaltenNr%3; | ||
//System.out.println("Start: ("+startZeile+"|"+startSpalte+")"); | //System.out.println("Start: ("+startZeile+"|"+startSpalte+")"); | ||
for(int zeile = startZeile; zeile<startZeile+3; zeile++){ | |||
for(int spalte = startSpalte; spalte<startSpalte+3; spalte++){ | for(int spalte = startSpalte; spalte<startSpalte+3; spalte++){ | ||
int z= zahlen[zeile][spalte]; | int z= zahlen[zeile][spalte]; | ||
| Zeile 499: | Zeile 512: | ||
return true; | return true; | ||
} | } | ||
/** | /** | ||
* prueft, ob pZahl an der Position moeglich ist. | * prueft, ob pZahl an der Position moeglich ist. | ||
| Zeile 528: | Zeile 540: | ||
return true; | return true; | ||
} | } | ||
'''public int belegteFelder(){''' | |||
int ergebnis = 0; | |||
for(int zeile=0; zeile<9; zeile++){ | |||
for(int spalte=0; spalte<9; spalte++){ | |||
if(zahlen[zeile][spalte] != 0){ | |||
ergebnis++; | |||
} | |||
} | |||
} | |||
return ergebnis; | |||
} | |||
/** | /** | ||
* berechnet, wie viele Moeglichkeiten es fuer dieses Feld gibt. | * berechnet, wie viele Moeglichkeiten es fuer dieses Feld gibt. | ||
| Zeile 550: | Zeile 574: | ||
return ergebnis; | return ergebnis; | ||
} | } | ||
/** | /** | ||
* bestimmt das Feld mit den wenigsten Moeglichkeiten. | * bestimmt das Feld mit den wenigsten Moeglichkeiten. | ||
| Zeile 573: | Zeile 597: | ||
return minFeld; | return minFeld; | ||
} | } | ||
/** | /** | ||
* | * | ||
| Zeile 582: | Zeile 606: | ||
'''public void eintragen(int zahl, int zeile, int spalte){''' | '''public void eintragen(int zahl, int zeile, int spalte){''' | ||
zahlen[zeile][spalte] = zahl; | zahlen[zeile][spalte] = zahl; | ||
} | } | ||
} | } | ||
</code> | |||
</code> | |||
Aktuelle Version vom 16. Januar 2023, 17:54 Uhr
nur relevant für den Leistungskurs!
Erklärvideos
Idee
Der folgende Text ist gekürzt aus der Wikipedia [1] übernommen.
Backtracking geht nach dem Versuch-und-Irrtum-Prinzip (trial and error) vor, das heißt, es wird versucht, eine erreichte Teillösung zu einer Gesamtlösung auszubauen. Wenn absehbar ist, dass eine Teillösung nicht zu einer endgültigen Lösung führen kann, wird der letzte Schritt beziehungsweise werden die letzten Schritte zurückgenommen, und es werden stattdessen alternative Wege probiert. Auf diese Weise ist sichergestellt, dass alle in Frage kommenden Lösungswege ausprobiert werden können
Backtracking wird am einfachsten rekursiv implementiert.
Beschreibung des Algorithmus
Die folgende Beschreibung ist gekürzt und leicht verändert aus der Wikipedia [2] übernommen.
Teillösung ist zu Anfang leer.
Stufe ist 0.
Funktion FindeLoesung (Stufe, Teillösung)
1. Abbruchbedingung: Wenn die Stufe zu groß ist
oder es keinen Teil-Lösungsschritt mehr gibt.
2. Abbruchbedingung: Wenn eine Lösung erreicht wurde.
Bearbeite ggf. die Lösung!
3. wiederhole, solange es noch neue Teil-Lösungsschritte gibt:
a) Wähle einen neuen Teil-Lösungsschritt.
b) Erweitere Teillösung um Wahl.
c) rekursiver Aufruf: FindeLoesung(Stufe+1, Teillösung)
d) Mache die Erweiterung der Teillösung rückgängig
Backtracking für kürzeste Wege auf Graphen
Um kürzeste Wege auf Graphen zu bestimmen, kann man den Backtracking-Algorithmus verwenden. Allerdings ist dieser sehr langsam; effizienter wird das Problem mit dem Dijkstra-Algorithmus gelöst.
Beispiel
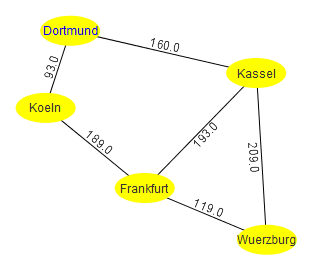
Gesucht ist die kürzeste Verbindung von Frankfurt nach Dortmund
Damit man keine Möglichkeit auslässt, geht man nach einer Ordnung vor - hier bietet es sich an, die möglichen Nachbarstädte nach dem Alphabet zu betrachten.
Dann ergibt sich für das Backtracking folgende Reihenfolge:
- Frankfurt -> Kassel -> Dortmund: merken!
- Frankfurt -> Kassel -> Würzburg: Sackgasse
- Frankfurt -> Köln -> Dortmund: kürzer, also merken!
- Frankfurt -> Würzburg -> Kassel -> Dortmund: länger, also ignorieren
Backtracking-Algorithmus für den kürzesten Weg
Man braucht die folgenden Attribute:
besterWeg: Hier wird der jeweils beste gefundene Weg gespeichert.besteLaenge: Die Länge vonbesterWegaktuellerWeg: Der Weg, der gerade untersucht wird.aktuelleLaenge: Die Länge vonaktuellerWeg
Mithilfe dieser lässt sich der Algorithmus so beschreiben:
findeKuerzestenWegBacktracking (pNode)
Abbruchbedingung:
Wenn pNode das Ziel ist (d.h. der Lösungsvektor ist vollständig!)
dann vergleiche aktuellerWeg mit besterWeg
und aktualisiere diesen, wenn es nötig ist.
Betrachte der Reihe nach alle Nachbarn von pNode.
Für jeden Nachbarn wird folgendes getan:
- den Nachbar zu aktuellerWeg hinzufügen (d.h. der Lösungsvektor wird erweitert!)
- aktuelleLaenge entsprechend erhöhen
- den Nachbarn markieren
- findeKuerzstestenWegBacktracking (nachbar) aufrufen
- die Änderungen wieder rückgängig machen (d.h. die Wahl wird rückgängig gemacht!)
- den Nachbarn aus aktuellerWeg entfernen
- aktuelleDistanz wieder zurücksetzen
- die Markierung des Nachbarn entfernen
Implementierung
Die Implementierung setzt auf die Klasse Graph auf.
Damit während des Backtracking auf die wesentlichen Daten zugegriffen werden kann, werden diese in Attributen gespeichert.
Die wesentlichen Methoden sind die folgenden:
- die Rahmenmethode
kuerzestenWegFinden(String pStart, String pZiel): In der Rahmenmethode wird alles für das rekursive Backtracking vorbereitet. - die rekursive Backtracking-Methode
kuerzestenWegFindenBacktracking(GraphNode pNode)
// Attribute
public GraphWithViewer graph;
// Attribute fuer das Backtracking
public ListWithViewer<Vertex> besterWeg;
public ListWithViewer<Vertex> aktuellerWeg;
public int besteLaenge;
public int aktuelleLaenge;
public Vertex start;
public Vertex ziel;
//Methoden
/**
* Kopiert den Inhalt einer Liste in eine andere Liste.
* Der Inhalt der Ziel-Liste wird dabei ersetzt.
* @param herkunftsListe
* @param zielListe
*/
private void kopiereListeIn(List herkunftsListe, List zielListe){
// besterWeg leeren
for(zielListe.toFirst();!zielListe.isEmpty();){
zielListe.remove();
}
// aktuellerWeg in besterWeg kopieren
for(herkunftsListe.toFirst();herkunftsListe.hasAccess();herkunftsListe.next()){
zielListe.append(herkunftsListe.getContent());
}
}
public ListWithViewer<Vertex> kuerzestenWegFinden(String pStart, String pZiel){
graph.setAllEdgeMarks(false);
start = graph.getVertex(pStart);
ziel = graph.getVertex(pZiel);
besterWeg = new ListWithViewer<>();
aktuellerWeg = new ListWithViewer<>();
besteLaenge = 10000000;
aktuelleLaenge = 0;
start.setMark(true);
aktuellerWeg.append(start);
kuerzestenWegFindenBacktracking(start);
return besterWeg;
}
private void kuerzestenWegFindenBacktracking(Vertex pNode) {
if(pNode.equals(ziel)){
if(aktuelleLaenge < besteLaenge){
// aktuellerWeg in besterWeg kopieren
kopiereListeIn(aktuellerWeg,besterWeg);
besteLaenge = aktuelleLaenge;
}
return;
}
List<Vertex> nachbarn = graph.getNeighbours(pNode);
for(nachbarn.toFirst(); nachbarn.hasAccess(); nachbarn.next()){
Vertex derNachbar = nachbarn.getContent();
if(!derNachbar.isMarked()){
derNachbar.setMark(true);
aktuellerWeg.append(derNachbar);
double distanz = graph.getEdge(derNachbar, pNode).getWeight();
aktuelleLaenge += distanz;
kuerzestenWegFindenBacktracking(derNachbar);
aktuelleLaenge -= distanz;
aktuellerWeg.toLast();
aktuellerWeg.remove();
derNachbar.setMark(false);
}
}
return;
}
Backtracking für Arrays: Magisches Quadrat
In ein magisches Quadrat werden die Zahlen von 1 bis 9 (bzw. 1 bis 16, 1 bis 25, ...) eingetragen. Die Summe muss in jeder Zeile, Spalte und Diagonale gleich sein.
Lösungen dieses Problems lassen sich gut mit Backtracking finden.
Implementierung
Die folgende Implementierung löst ein 3x3 Quadrat.
- Als Datenstruktur muss nur das Quadrat bereitgestellt werden, das ein 3x3-Array ist.
- Die Stufen des Backtracking-Verfahrens sind hier die Felder; dabei gehen die Stufen von 0 bis 8.
- Aus der Stufe kann man die Koordinaten des Feldes berechnen.
- Das eigentliche Backtracking findet in der Methode
public void findeLoesung(int pStufe)statt; diese Methode wird von der Rahmenmethodepublic void findeLoesung()aufgerufen.
public class MagischesQuadratFertig {
private int[][] quadrat;
MagischesQuadratFertig(){
quadrat = new int[3][3];
initialisiere();
}
public void initialisiere(){
for ( int y=0 ; y < 3 ; y++ ) {
for ( int x=0 ; x < 3 ; x++ ) {
quadrat[x][y] = 0;
}
}
}
public void findeLoesung(){
findeLoesung(0);
System.out.println("*** Loesung: ***");
this.ausgeben();
}
//Die eigentliche Backtracking-Methode!
public boolean findeLoesung(int pStufe){
ausgeben();
// Abbruch, wenn pStufe ueber das Quadrat hinausgeht.
if(pStufe == 3*3){
return false;
}
// aus pStufe die x-Koordinate und die y-Koordinate berechnen
int x = pStufe % 3;
int y = pStufe / 3;
// jetzt fuer pStude alle Moeglichkeiten durchlaufen,
// d.h. die Zahlen von 1 bis 9
for(int i=1; i<= 3*3; i++){
// die Zahl i an die richtige Stelle in das Quadrat eintragen
quadrat[x][y] = i;
// Wenn es die Zahl schon einmal gibt, dann zur naechsten Zahl weiter.
if(esGibtDoppelte()){
continue;
}
// wenn man ein magisches Quadrat gefunden hat, dann true zurueckgeben.
if(magisch()){
return true;
}
// es gibt keine Doppelten, aber das Quadrat ist (noch) nicht magisch
// d.h. man baut die Teilloesung weiter aus.
// Dafuer ein rekursiver Aufruf fuer die naechsthoehere Stufe.
// Der Aufruf gibt zurueck, ob das Ausbauen der Teilloesung zum Erfolg fuehrte.
boolean fertig = findeLoesung(pStufe + 1);
if(fertig){
return true;
}
} // end for
// Auf dieser Stufe wurden alle Zahlen von 1 bis 9 durchprobiert, ohne Erfolg.
// Man loescht die Information auf dieser Stufe...
quadrat[x][y] = 0;
// und gibt false zurueck
return false;
}
public boolean esGibtDoppelte(){
boolean[] dabei = new boolean[3*3+1];
for ( int y=0 ; y < 3 ; y++ ) {
for ( int x=0 ; x < 3 ; x++ ) {
int index = quadrat[x][y];
if(index != 0 && dabei[index]){
return true;
}
dabei[index] = true;
}
}
return false;
}
public boolean magisch(){
if(esGibtDoppelte()){
return false;
}
// Summen testen
int s=0, t=0;
// 1. Diagonale
for ( int x=0 ; x < 3 ; x++ ) s+=quadrat[x][x];
//2. Diagonale
for ( int x=0 ; x < 3 ; x++ ) t+=quadrat[3-x-1][x];
if (t != s) return false;
// Zeilen
for ( int y=0 ; y < 3 ; y++ ) {
int k=0;
for ( int x=0 ; x < 3 ; x++ ) {
k += quadrat[x][y];
}
if (k != s) return false;
}
for ( int x=0 ; x < 3 ; x++ ) {
int k=0;
for ( int y=0 ; y < 3 ; y++ ) {
k += quadrat[x][y];
}
if (k != s) return false;
}
System.out.println("*** It's magic!!! ***");
return true;
}
public void ausgeben(){
for ( int y=0 ; y < 3 ; y++ ) {
for ( int x=0 ; x < 3 ; x++ ) {
System.out.print(quadrat[x][y]);
}
System.out.print(" ");
}
System.out.println();
}
public static void main(String[] args) {
MagischesQuadratFertig mq = new MagischesQuadratFertig();
mq.findeLoesung();
}
}
Aufgabe: Backtracking für Arrays: Rucksackproblem selber programmieren
Das Rucksackproblem lässt anhand des folgenden Beispiels beschreiben:
- In einen Rucksack kann man 200kg laden (=ganz schön schwer...).
- Es gibt die folgenden Gewichte: 28, 57, 33, 18, 99, 42, 17, 52
- Welche Gewichte muss man in den Rucksack laden, damit die 200kg möglichst gut ausgenutzt, aber nicht überschritten werden?
Implementierung zum Selbermachen
Die folgende Implementierung hält neben gewichte und maxGewicht noch folgende Datenstrukturen bereit:
boolean[] teilLoesung: In diesem Array wird festgehalten, welche der Gewichte bei der aktuell untersuchten Lösung dabei sind.boolean[] besteLoesung: In diesem Array wird die bisher beste Lösung festgehalten.
Diese Variablen müssen natürlich im Laufe des Backtracking immer aktualisiert werden.
Die Implementierung ist noch nicht vollständig; der Backtracking-Teil muss hier noch programmiert werden; dafür muss die Methode sucheBesteLoesung(int pStufe) ergänzt werden.
Viel Spaß beim Programmieren!
public class Rucksackproblem {
public int[] gewichte = {28, 57, 33, 18, 99, 42, 17, 52};
public int maxGewicht = 200;
public boolean[] teilLoesung = new boolean[gewichte.length];
public boolean[] besteLoesung = new boolean[gewichte.length];
public void sucheBesteLoesung(){
//Vorbereitung
for(int i=0; i<teilLoesung.length; i++){
teilLoesung[i] = false;
}
kopiereInBesteLoesung();
// los gehts!
sucheBesteLoesung(0);
System.out.println("*** Beste Loesung: ***");
ausgeben(besteLoesung);
}
public void sucheBesteLoesung(int pStufe) {
teilLoesungAusgeben();
//TODO
}
public void ausgeben(boolean[] b){
System.out.print(berechneGewicht(b)+": ");
for(int i=0; i<b.length; i++){
if(b[i]){
System.out.print(gewichte[i]+",");
}
}
System.out.println();
}
public void teilLoesungAusgeben(){
for(int i=0; i<teilLoesung.length; i++){
if(teilLoesung[i]){
System.out.print("+");
}
else{
System.out.print("-");
}
}
System.out.println();
}
public void kopiereInBesteLoesung(){
for(int i=0; i<teilLoesung.length; i++){
besteLoesung[i] = teilLoesung[i];
}
}
public int berechneGewicht(boolean[] b){
int ergebnis = 0;
for(int i=0; i<b.length; i++){
if(b[i]){
ergebnis += gewichte[i];
}
}
return ergebnis;
}
public static void main(String[] args) {
Rucksackproblem rp = new Rucksackproblem();
rp.sucheBesteLoesung();
}
}
Aufgabe: Backtracking zum Lösen von Sudokus
Wer hat nicht schon mal entnervt beim Lösen eines Sudokus den Bleistift bis auf den Stummel runtergeschrieben?!
Abhilfe schafft hier ein geeignetes Java-Programm!
Die "langweiligen" Hilfsmethoden sind unten schon programmiert - es fehlt nur noch die Methode loesenMitBacktracking(int pStufe).
Hinweise:
- Die "Teillösung" muss man nicht als Parameter der Backtracking-Methode übergeben, weil immer das Array
zahlenentsprechend aktualisiert wird.
- Die "Stufe" beginnt nicht bei 0, sondern bei der Anzahl der belegten Felder. Dann kann der Backtracking-Algorithmus abbrechen, sobald man die Stufe 81 erreicht.
public class Sudoku {
// Das "schwerste Sudoku der Welt"
// https://www.oe24.at/welt/Das-ist-das-schwierigste-Sudoku-der-Welt/1597831
int[][] zahlen = {
{0,0,5,3,0,0,0,0,0},
{8,0,0,0,0,0,0,2,0},
{0,7,0,0,1,0,5,0,0},
{4,0,0,0,0,5,3,0,0},
{0,1,0,0,7,0,0,0,6},
{0,0,3,2,0,0,0,8,0},
{0,6,0,5,0,0,0,0,9},
{0,0,4,0,0,0,0,3,0},
{0,0,0,0,0,9,7,0,0}
};
public static void main(String[] args) {
Sudoku s = new Sudoku();
System.out.println("*** Aufgabe ***");
s.ausgeben();
int belegteFelder = s.belegteFelder();
boolean erfolg = s.loesenMitBacktracking(belegteFelder);
if(erfolg == true){
System.out.println("Loesung gefunden!");
}
else{
System.out.println("keine Loesung");
}
}
public boolean loesenMitBacktracking(int pStufe){
//TODO
return false;
}
private void ausgeben() {
String trennlinie = "+---+---+---+";
for(int zeile = 0; zeile<9; zeile++){
if(zeile%3 == 0){
System.out.println(trennlinie);
}
for(int spalte=0; spalte<9; spalte++){
if(spalte%3 == 0){
System.out.print("|");
}
System.out.print(zahlen[zeile][spalte]);
}
System.out.println("|");
}
System.out.println(trennlinie);
System.out.println();
}
public boolean istOkZeile(int pZeilenNr){
boolean[] verwendeteZahlen = new boolean[10];
for(int spalte = 0; spalte<9; spalte++){
int z= zahlen[pZeilenNr][spalte];
if(z!=0){
if(verwendeteZahlen[z] == true){
return false;
}
verwendeteZahlen[z] = true;
}
}
return true;
}
public boolean istOkSpalte(int pSpaltenNr){
boolean[] verwendeteZahlen = new boolean[10];
for(int zeile = 0; zeile<9; zeile++){
int z= zahlen[zeile][pSpaltenNr];
if(z!=0){
if(verwendeteZahlen[z] == true){
return false;
}
verwendeteZahlen[z] = true;
}
}
return true;
}
/**
* ueberprueft, ob das Quadrat ok ist,
* in dem (pZeilenNr|pSpaltenNr) liegt.
* @param pZeilenNr
* @param pSpaltenNr
* @return
*/
public boolean istOkQuadrat(int pZeilenNr, int pSpaltenNr){
boolean[] verwendeteZahlen = new boolean[10];
int startZeile = pZeilenNr - pZeilenNr%3;
int startSpalte = pSpaltenNr - pSpaltenNr%3;
//System.out.println("Start: ("+startZeile+"|"+startSpalte+")");
for(int zeile = startZeile; zeile<startZeile+3; zeile++){
for(int spalte = startSpalte; spalte<startSpalte+3; spalte++){
int z= zahlen[zeile][spalte];
if(z!=0){
if(verwendeteZahlen[z] == true){
return false;
}
verwendeteZahlen[z] = true;
}
}
}
return true;
}
/**
* prueft, ob pZahl an der Position moeglich ist.
* Veraendert zahlen aber nicht!
* @param pZahl
* @param pZeilenNr
* @param pSpaltenNr
* @return
*/
public boolean istMoeglich(int pZahl, int pZeilenNr, int pSpaltenNr){
// den Wert auslesen, um ihn hinterher wieder herstellen zu koennen.
int z = zahlen[pZeilenNr][pSpaltenNr];
zahlen[pZeilenNr][pSpaltenNr] = pZahl;
if(!istOkZeile(pZeilenNr)){
zahlen[pZeilenNr][pSpaltenNr] = z;
return false;
}
if(!istOkSpalte(pSpaltenNr)){
zahlen[pZeilenNr][pSpaltenNr] = z;
return false;
}
if(!istOkQuadrat(pZeilenNr, pSpaltenNr)){
zahlen[pZeilenNr][pSpaltenNr] = z;
return false;
}
zahlen[pZeilenNr][pSpaltenNr] = z;
return true;
}
public int belegteFelder(){
int ergebnis = 0;
for(int zeile=0; zeile<9; zeile++){
for(int spalte=0; spalte<9; spalte++){
if(zahlen[zeile][spalte] != 0){
ergebnis++;
}
}
}
return ergebnis;
}
/**
* berechnet, wie viele Moeglichkeiten es fuer dieses Feld gibt.
* Wenn in dem Feld eine Zahl > 0 steht, dann wird sofort 0 zurueckgegeben.
* @param pZeilenNr
* @param pSpaltenNr
* @return
*/
public int wievieleMoeglichkeiten(int pZeilenNr, int pSpaltenNr){
int ergebnis = 0;
if(zahlen[pZeilenNr][pSpaltenNr] > 0){
return 0;
}
for(int z=1; z<=9; z++){
if(istMoeglich(z, pZeilenNr, pSpaltenNr)){
//System.out.print(z);
ergebnis++;
}
}
//System.out.println();
return ergebnis;
}
/**
* bestimmt das Feld mit den wenigsten Moeglichkeiten.
* Wenn es kein Feld mit Moeglichkeiten mehr gibt, wird {-1,-1} zurueckgegeben.
* @return ein Array mit 2 Eintraegen: Index 0: zeile; Index 1: spalte
*/
public int[] feldMitDenWenigstenMoeglichkeiten(){
int[] minFeld = {-1,-1};
int minMoeglichkeiten = 1000;
for(int zeile=0; zeile<9; zeile++){
for(int spalte=0; spalte<9; spalte++){
int moeglichkeiten = wievieleMoeglichkeiten(zeile, spalte);
// es werden nur Felder beruecksichtigt,
// fuer die es mindestens eine Moeglichkeit gibt.
if(moeglichkeiten > 0 && moeglichkeiten < minMoeglichkeiten){
minMoeglichkeiten = moeglichkeiten;
minFeld[0] = zeile;
minFeld[1] = spalte;
}
}
}
return minFeld;
}
/**
*
* @param zahl
* @param zeile
* @param spalte
*/
public void eintragen(int zahl, int zeile, int spalte){
zahlen[zeile][spalte] = zahl;
}
}