Nicht-deterministischer endlicher Automaten: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
| Zeile 7: | Zeile 7: | ||
* '''Die Übergänge zwischen den Zuständen sind <u>nicht eindeutig</u>.'''<br/>D.h. es kann für ein Symbol und einen Zustand mehrere mögliche Übergänge geben. | * '''Die Übergänge zwischen den Zuständen sind <u>nicht eindeutig</u>.'''<br/>D.h. es kann für ein Symbol und einen Zustand mehrere mögliche Übergänge geben. | ||
* '''Ein Wort gilt als akzeptiert, wenn es für das Wort einen Übergang vom Anfangs- in einen Endzustand <u>gibt</u>.'''<br/>D.h.: Nicht jeder "Weg" muss zu einem Endzustand führen - es reicht, wenn es einen Weg gibt! <br/>''Und der "richtige" Weg ist manchmal ziemlich schwer zu finden...'' | * '''Ein Wort gilt als akzeptiert, wenn es für das Wort einen Übergang vom Anfangs- in einen Endzustand <u>gibt</u>.'''<br/>D.h.: Nicht jeder "Weg" muss zu einem Endzustand führen - es reicht, wenn es einen Weg gibt! <br/>''Und der "richtige" Weg ist manchmal ziemlich schwer zu finden...'' | ||
=Fachbegriffe= | |||
Nicht-Deterministischer endlicher Automat (NEA), Zustand, Anfangszustand, Endzustände, Alphabet, Übergang, Zustandsübergangsfunktion, Übergangsgraph, prüfen, "es gibt einen Weg" | |||
=Beispiel= | =Beispiel= | ||
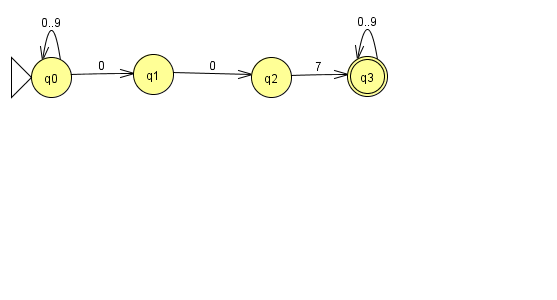
[[File:Automat007nichtDeterministisch.png|thumb|Der KGB-Automat als <u>Nicht</u>-deterministischer endlicher Automat. |557px]] | [[File:Automat007nichtDeterministisch.png|thumb|Der KGB-Automat als <u>Nicht</u>-deterministischer endlicher Automat. |557px]] | ||
Version vom 23. Juni 2019, 13:47 Uhr
Nichtdeterministische endliche Automaten unterscheiden sich von Deterministischen endlichen Automaten in zwei wesentlichen Punkten:
- Die Übergänge zwischen den Zuständen sind nicht eindeutig.
D.h. es kann für ein Symbol und einen Zustand mehrere mögliche Übergänge geben. - Ein Wort gilt als akzeptiert, wenn es für das Wort einen Übergang vom Anfangs- in einen Endzustand gibt.
D.h.: Nicht jeder "Weg" muss zu einem Endzustand führen - es reicht, wenn es einen Weg gibt!
Und der "richtige" Weg ist manchmal ziemlich schwer zu finden...
Fachbegriffe
Nicht-Deterministischer endlicher Automat (NEA), Zustand, Anfangszustand, Endzustände, Alphabet, Übergang, Zustandsübergangsfunktion, Übergangsgraph, prüfen, "es gibt einen Weg"
Beispiel
Der KGB-Automat erkennt Wörter, die nur aus den Ziffern 0,...,9 bestehen und die irgendwo die Zahlenkette "007" enhalten.
Man sieht, dass im Zustand q0 der Übergang für die 0 nicht eindeutig ist; man kann entweder bei q0 bleiben oder zu q1 übergehen.
Die Darstellung als Nicht-deterministischer endlicher Automat ist oft viel einfacher als die Darstellung als Deterministischer Endlicher Automat.
Beziehung zu deterministischen endlichen Automaten
- Jeder deterministische endliche Automat ist (ohne irgendwelches Dazutun) direkt auch ein Nicht-deterministischer endlicher Automat.
- Zu jedem Nicht-deterministischen endlichen Automaten kann man eine deterministischen endlichen Automaten konstruieren.
- Das Verfahren dazu heißt Potenzmengenkonstruktion und ist reichlich kompliziert, funktioniert aber immer!
(Das ist mathematisch bewiesen...)
- Das Verfahren dazu heißt Potenzmengenkonstruktion und ist reichlich kompliziert, funktioniert aber immer!
Beziehung zu regulären Grammatiken
- Zu jedem nicht-deterministischen endlichen Automaten lässt sich einfach eine reguläre Grammatik konstruieren:
- Aus jedem Zustand des Automaten macht man ein Nicht-Terminal in der Grammatik - und der Rest ergibt sich von selbst.
- Zu jeder regulären Grammatik lässt sich einfach ein nicht-deterministischer endlicher Automat konstruieren:
- Aus jedem Nichtterminalsymbol wird einen Zustand des Automaten gemacht und aus jeder Produktionsregel einen Übergang des Automaten.
- Der Nicht-deterministische endliche Automat ist deswegen ein Zwischenschritt beim Übergang von der regulären Grammatik zum deterministischen endlichen Automaten.