Nicht-deterministischer endlicher Automaten

Nichtdeterministische endliche Automaten unterscheiden sich von Deterministischen endlichen Automaten in zwei wesentlichen Punkten:

• Die Übergänge zwischen den Zuständen sind nicht eindeutig.
  D.h. es kann für ein Symbol und einen Zustand mehrere mögliche Übergänge geben.
• Ein Wort gilt als akzeptiert, wenn es für das Wort einen Übergang vom Anfangs- in einen Endzustand gibt.
  D.h.: Nicht jeder "Weg" muss zu einem Endzustand führen - es reicht, wenn es einen Weg gibt!
  Und der "richtige" Weg ist manchmal ziemlich schwer zu finden...

Fachbegriffe

Nicht-Deterministischer endlicher Automat (NEA), Zustand, Anfangszustand, Endzustände, Alphabet, Übergang, Zustandsübergangsfunktion, Übergangsgraph, prüfen, "es gibt einen Weg"

Beispiel

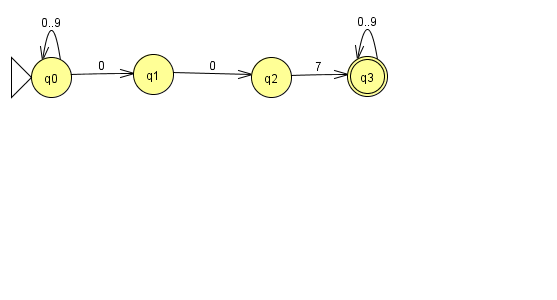
Der KGB-Automat als Nicht-deterministischer endlicher Automat.

Der KGB-Automat erkennt Wörter, die nur aus den Ziffern 0,...,9 bestehen und die irgendwo die Zahlenkette "007" enhalten.

Man sieht, dass im Zustand q0 der Übergang für die 0 nicht eindeutig ist; man kann entweder bei q₀ bleiben oder zu q₁ übergehen.

Die Darstellung als Nicht-deterministischer endlicher Automat ist oft viel einfacher als die Darstellung als Deterministischer Endlicher Automat.

Beziehung zu deterministischen endlichen Automaten

• Jeder deterministische endliche Automat ist (ohne irgendwelches Dazutun) direkt auch ein Nicht-deterministischer endlicher Automat.
• Zu jedem Nicht-deterministischen endlichen Automaten kann man eine deterministischen endlichen Automaten konstruieren.
  • Das Verfahren dazu heißt Potenzmengenkonstruktion und ist reichlich kompliziert, funktioniert aber immer!
    (Das ist mathematisch bewiesen...)

Zustandsfolgen für NEAs

Wenn prüfen will, ob ein Wort von einem NEA erkannt wird, dann muss man jede der (nicht deterministischen) Möglichkeiten durchprüfen!
Das gilt vor allem, wenn man zeigen will, dass ein Wort nicht akzeptiert wird.

Beispiel: Das Wort 70008: Prüfung mit Zustandsfolgen

   7     0     0     0     8
q0 -> q0 -> q0 -> q0 -> q0 -> q0    kein Endzustand erreicht. 
q0 -> q0 -> q0 -> q0 -> q1 ->       Senke
q0 -> q0 -> q0 -> q1 -> q2 ->       Senke
q0 -> q0 -> q1 -> q2 ->             Senke
 
Damit ist gezeigt, dass "70008" nicht akzeptiert wird.

Man sieht - das ist sehr aufwändig - und das umso mehr, je komplizierter der Automat wird.

Bei diesem Automat kann man natürlich durch logische Überlegungen schnell ermitteln, dass "70008" nicht akzeptiert wird, aber das geht ja nicht immer.
Deswegen lohnt es sich, eine nicht-deterministische Zustandsfolge zur Überprüfung von Wörtern zu nutzen!

Nicht-deterministische Zustandsfolgen

Bei einer nicht-deterministischen Zustandsfolge schreibt man nach jedem Zeichen alle möglichen Zustände auf.

Beispiel: Das Wort 70008 - Prüfung mit einer nicht-deterministischen Zustandsfolge

   7       0          0             0             8 
q0 -> {q0} -> {q0,q1} -> {q0,q1,q2} -> {q0,q1,q2} -> {q0}           

Die Menge nach der Abarbeitung des Wortes "70008" enthält nur den Zustand q0.
Das heißt: Es gibt keinen Weg zu einem Endzustand, und damit ist das Wort nicht akzeptiert.

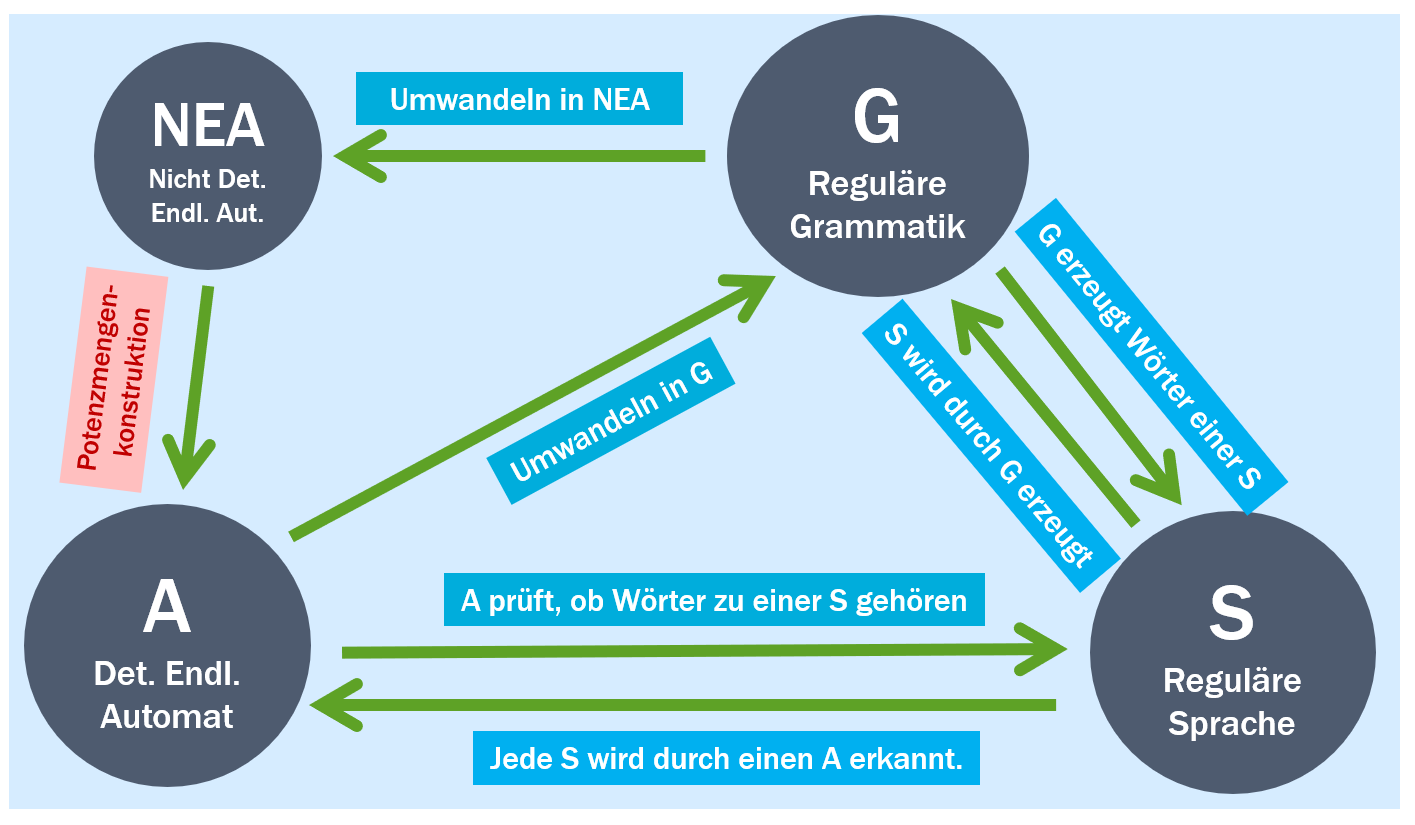
Beziehung zu regulären Grammatiken

Beziehungen: Reguläre Grammatik - DEA - NEA - reguläre Sprache

• Zu jedem nicht-deterministischen endlichen Automaten lässt sich einfach eine reguläre Grammatik konstruieren:
  • Aus jedem Zustand des Automaten macht man ein Nicht-Terminal in der Grammatik - und der Rest ergibt sich von selbst.
• Zu jeder regulären Grammatik lässt sich einfach ein nicht-deterministischer endlicher Automat konstruieren:
  • Aus jedem Nichtterminalsymbol wird einen Zustand des Automaten gemacht und aus jeder Produktionsregel einen Übergang des Automaten.
  • Der Nicht-deterministische endliche Automat ist deswegen ein Zwischenschritt beim Übergang von der regulären Grammatik zum deterministischen endlichen Automaten.