Kellerautomat

nur relevant für den Leistungskurs!

Ein Kellerautomat ist ein Deterministischer Endlicher Automat (DEA), der um einen Speicher (genannt Keller) in Form eines Stack erweitert wurde. In dem Keller kann der Kellerautomat Zeichen, die im sogenannten Kelleralphabet definiert sind, speichern und sie später nach dem Last-In-First-Out-Prinzip wieder abrufen.

Fachbegriffe

Alphabet, Zeichen, Kelleralphabet, Kellerzeichen, Zustand, Anfangszustand, Endzustände, Übergang

Zweck des Kellerautomaten

Deterministische Endliche Automaten können nur sehr begrenzte Sprachen überprüfen, vor allem deswegen, weil sie nicht "zählen" können. Deswegen ist z.B. die Sprache L = {aⁿbⁿ} mit einem DEA nicht darstellbar.

Ein Kellerautomat kann diese Sprache überprüfen!

Beispiel

Kellerautomat für die Sprache L = {aⁿbⁿ}.

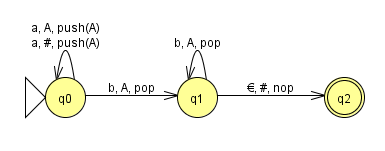
Der folgende Kellerautomat überprüft die Sprache L = {aⁿbⁿ}.

Erläuterung:

• Q = {q₀, q₁, q₂}
• A = {a, b}
• K = {#, A}
  dabei ist # das Anfangssymbol im Keller (d.h. es steht für einen leeren Keller)
• d: siehe rechts
• Startzustand: q₀
• F = {q₂} ist die Menge der Endzustände

Formale Definition des Kellerautomaten

Der Kellerautomat ist ein 7-Tupel (Q, A, K, d, q₀, #, F)

Dabei ist:

• Q: endliche Menge von Zuständen = {q₀, ..., q_n}
• A: Das endliche Eingabealphabet
• K: das endliche Kelleralphabet
• d: die Übergangsfunktion:
  Sie berechnet aus einem Zustand, einem Eingabezeichen und einem Kellerzeichen
  einen Nachfolgezustand und eine Kelleroperation
• q₀ist der Startzustand.
• # ist das Anfangssymbol im Keller
• F ist die Menge der akzeptierenden Endzustände.

Zusammenhang zur kontextfreien Grammatik

• Der deterministische Kellerautomat erkennt genau die deterministisch-kontextfreien Sprachen.
• Der nichtdeterministische Kellerautomat erkennt genau die kontextfreien Sprachen, d.h. Sprachen, die von einer kontextfreien Grammatik erzeugt werden.

Parser für einen Kellerautomaten

Die folgende Programmierung realisiert den Übergangsgraphen (s.o.) in Java:

   public boolean parse(String pWort){
       // ein € anhaengen
       // erleichtert die Ueberpruefung des Endes!
       pWort += '€';
       Stack<Character> keller = new StackWithViewer<Character>();
       keller.push('#');
       int zustand = 0;
       for(int i=0; i<pWort.length(); i++){
           char zeichen = pWort.charAt(i);
           char kellerzeichen = keller.top();
           switch(zustand){
               case 0:
                   if(zeichen=='a' && kellerzeichen == '#'){
                       zustand = 0;
                       keller.push('A');
                   }
                   else if(zeichen=='a' && kellerzeichen == 'A'){
                       zustand = 0;
                       keller.push('A');
                   }
                   else if(zeichen =='b' && kellerzeichen == 'A'){
                       zustand = 1;
                       keller.pop();
                   }
                   else{
                       return false;
                   }
                   continue;                   
                   // end case 0
               case 1:
                   if(zeichen=='b' && kellerzeichen == 'A'){
                       zustand = 1;
                       keller.pop();
                   }
                   else if(zeichen=='€' && kellerzeichen == '#'){
                       zustand = 2;
                   }
                   else{
                       return false;
                   }
                   continue;
                   // end case 1
           }    // end switch(zustand)
       }    // end for
    
       // Das Wort ist abgearbeitet!
       // Ueberpruefen, ob Endzustand erreicht
       return (zustand == 2);
   }