Kellerautomat
nur relevant für den Leistungskurs!
Ein Kellerautomat ist ein Deterministischer Endlicher Automat (DEA), der um einen Speicher (genannt Keller) in Form eines Stack erweitert wurde. In dem Keller kann der Kellerautomat Zeichen, die im sogenannten Kelleralphabet definiert sind, speichern und sie später nach dem Last-In-First-Out-Prinzip wieder abrufen.
Fachbegriffe
Alphabet, Zeichen, Kelleralphabet, Kellerzeichen, Zustand, Anfangszustand, Endzustände, Übergang
Zweck des Kellerautomaten
Deterministische Endliche Automaten können nur sehr begrenzte Sprachen überprüfen, vor allem deswegen, weil sie nicht "zählen" können. Deswegen ist z.B. die Sprache L = {anbn} mit einem DEA nicht darstellbar.
Ein Kellerautomat kann diese Sprache überprüfen!
Beispiel
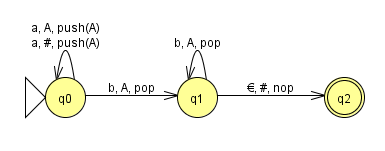
Die Darstellung rechts entspricht der "SIBI-internen" Schreibweise.
So darf man in Klausuren schreiben!
Die Standard-Schreibweise (s.u.) muss man aber mindestens lesen können.
Der folgende Kellerautomat überprüft die Sprache L = {anbn}.
Erläuterung:
- Q = {q0, q1, q2}
- A = {a, b}
- K = {#, A}
dabei ist # das Anfangssymbol im Keller (d.h. es steht für einen leeren Keller) - d: siehe rechts
- Startzustand: q0
- F = {q2} ist die Menge der Endzustände
Beispiel in Standard-Schreibweise
Die Standard-Schreibweise wird im Zentralabitur, aber auch von Wikipedia genutzt.
Die Standard-Schreibweise muss man mindestens lesen können.
Zum Schreiben ist auch die SIBI-interne Schreibweise (s.o.) möglich.
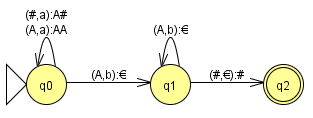
Der Zustandsübergangsgraph rechts zeigt die Standard-Schreibweise für einen Kellerautomaten, der die Sprache Sprache L = {anbn} überprüft.
Erläuterung:
- In der Klammer steht zuerst das aktuelle Kellerzeichen (d.h. das oberste Zeichen auf dem Keller-Stapel) und dann der Buchstabe des Wortes, der gerade bearbeitet wird.
- Nach dem Doppelpunkt steht der Zustand des Kellers nach Abarbeitung.
Dabei bedeutet...€: das oberste Zeichen im Keller wurde gelöscht (d.h.pop)- ein Buchstabe : der Keller hat sich nicht verändert (d.h.
nop). - zwei Buchstaben : es wurde ein Kellerzeichen oben in den Keller reingeschichtet.
Der erste der beiden Buchstaben ist das neue Kellerzeichen,
der zweite Buchstabe ist das bisherige oberste Kellerzeichen.
Formale Definition des Kellerautomaten
Der Kellerautomat ist ein 7-Tupel (Q, A, K, d, q0, #, F)
Dabei ist:
- Q: endliche Menge von Zuständen = {q0, ..., qn}
- A: Das endliche Eingabealphabet
- K: das endliche Kelleralphabet
- d: die Übergangsfunktion:
Sie berechnet aus einem Zustand, einem Eingabezeichen und einem Kellerzeichen
einen Nachfolgezustand und eine Kelleroperation - q0ist der Startzustand.
- # ist das Anfangssymbol im Keller
- F ist die Menge der akzeptierenden Endzustände.
Deterministischer und Nicht-Deterministischer Kellerautomat
Der nicht-deterministische Kellerautomat ist mächtiger als der deterministische Kellerautomat!
D.h. es gibt Sprachen, die von einem Nicht-Deterministischen Kellerautomaten geprüft werden können, nicht aber von einem Deterministischen Kellerautomaten.
Beispiel
Die von der kontextfreien Grammatik erzeugte Sprache
L = { 0S0 | 1S1 | ε }
kann zwar von einem nicht-deterministischen Kellerautomaten erkannt werden,
aber nicht von einem deterministischen Kellerautomaten.
Warum das so ist?! Das geht über das Geschehen auch im Informatik-LK hinaus.
Damit kann/muss man sich im Informatik-Studium (Vorlesung: Theoretische Informatik) auseinandersetzen...
Zusammenhang zur kontextfreien Grammatik
- Jede von einer kontextfreien Grammatik erzeugte Sprache lässt sich durch einen nicht-deterministischen Kellerautomat überprüfen.
- Zu jeder von einem nicht-deterministischen Kellerautomaten erkannten Sprache gibt es eine kontextfreie Grammatik.
Die Frage nach dem "Warum?" geht auch über den Informatik-LK hinaus und bleibt hier unbeantwortet.
Irgendetwas muss ja auch für das Studium noch übrig bleiben...
Parser für einen Kellerautomaten
Die folgende Programmierung realisiert den Übergangsgraphen (s.o.) in Java:
public boolean parse(String pWort){
// ein € anhaengen
// erleichtert die Ueberpruefung des Endes!
pWort += '€';
Stack<Character> keller = new StackWithViewer<Character>();
keller.push('#');
int zustand = 0;
for(int i=0; i<pWort.length(); i++){
char zeichen = pWort.charAt(i);
char kellerzeichen = keller.top();
if(zustand == 0){
if(zeichen=='a' && kellerzeichen == '#'){
zustand = 0;
keller.push('A');
}
else if(zeichen=='a' && kellerzeichen == 'A'){
zustand = 0;
keller.push('A');
}
else if(zeichen =='b' && kellerzeichen == 'A'){
zustand = 1;
keller.pop();
}
else{
return false;
}
continue;
// end case 0
else if(zustand == 1){
if(zeichen=='b' && kellerzeichen == 'A'){
zustand = 1;
keller.pop();
}
else if(zeichen=='€' && kellerzeichen == '#'){
zustand = 2;
}
else{
return false;
}
continue;
// end case 1
}
else{
// andere Zustaende, d.h. Zustand 2
System.err.println("Im Zustand 2 darf es kein Zeichen mehr geben!!");
return false;
}
} // end for
// Das Wort ist abgearbeitet!
// Ueberpruefen, ob Endzustand erreicht
return (zustand == 2);
}