Reguläre Grammatik: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „=Definition= Eine '''Grammatik''' G wird durch ein 4-Tupel (N, T, S, P) definiert: * N ist die Menge der '''Nichtterminalsymbole'''. * T ist die Menge der '''T…“) |
|||
| (24 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
=Definition= | [[Kategorie:endliche Automaten]] | ||
[[Kategorie:Informatik-Q2]] | |||
[[Kategorie:Informatik-Abitur]] | |||
[[Kategorie:Informatik]] | |||
=Fachbegriffe= | |||
Nicht-terminal-symbole, Terminal-Symbole, Startsymbol, Produktionsregeln, Ableitung (eines Wortes), Sprache | |||
=Erklärvideos= | |||
* [https://youtu.be/BcMXVx6VeSk Deterministischen endlichen Automaten in reguläre Grammatik umwandeln] | |||
=Definition Grammatik= | |||
Eine '''Grammatik''' G wird durch ein 4-Tupel (N, T, S, P) definiert: | Eine '''Grammatik''' G wird durch ein 4-Tupel (N, T, S, P) definiert: | ||
* N ist die Menge der '''Nichtterminalsymbole'''. | * N ist die Menge der '''Nichtterminalsymbole'''. | ||
| Zeile 5: | Zeile 17: | ||
* S ∈ N ist das '''Startsymbol'''. | * S ∈ N ist das '''Startsymbol'''. | ||
* P ist die Menge der '''Produktionsregeln'''. | * P ist die Menge der '''Produktionsregeln'''. | ||
=Reguläre Grammatik= | |||
Reguläre Grammatiken sind entweder '''rechtslinear''' oder '''linkslinear'''. | |||
"Üblich" sind rechtslineare Grammatiken, weil sie sich aus DEAs und NEAs direkt herstellen lassen. | |||
''' | Linkslineare Grammatiken sind '''äquivalent''' zu rechtslinearen Grammatiken, d.h.: | ||
* für jede linkslineare Grammatik gibt es eine rechtslineare Grammatik, die die gleiche Sprache erzeugt. | |||
* | * für jede rechtslineare Grammatik gibt es eine linkslineare Grammatik, die die gleiche Sprache erzeugt. | ||
* | |||
= | ==rechtslineare Grammatik== | ||
Eine '''rechtslineare''' Grammatik ist eine Grammatik, bei der <u>alle</u> Produktionen eine der folgenden Formen haben: | |||
* '''A → aB''' ''d.h. Nichtterminalsymbol wird ersetzt durch ein Terminalsymbol gefolgt von einem Nichtterminalsymbol''. '''Das Nicht-Terminal steht <u>rechts</u>.''' | |||
* A → a ''d.h. Nichtterminalsymbol wird ersetzt durch ein Terminalsymbol.'' | |||
* A → ε ''d.h. Nichtterminalsymbol wird ersetzt durch nichts. (ε steht für nichts.)'' | |||
=linkslineare Grammatiken= | |||
in '''linkslinearen''' Grammatiken haben alle Regeln die Form: | |||
* '''A → Ba''' ''d.h. Nichtterminalsymbol wird ersetzt durch ein Nichtterminalsymbol gefolgt von einem Terminalsymbol''. '''Das Nicht-Terminal steht <u>links</u>.''' | |||
* A → a ''d.h. Nichtterminalsymbol wird ersetzt durch ein Terminalsymbol.'' | |||
* A → ε ''d.h. Nichtterminalsymbol wird ersetzt durch nichts. (ε steht für nichts.)'' | |||
Das heißt: Der Unterschied zwischen regulären und linkslinearen Grammatiken besteht darin, dass bei den linkslinearen Grammatiken immer erst das Nichtterminalsymbol und dann das Terminalsymbol kommt. | |||
=Beispiele= | |||
==KGB-Sprache== | |||
Die KGB-Sprache besteht aus allen Ziffernfolgen, die irgendwo die Zahlenkette "007" enhalten. | Die KGB-Sprache besteht aus allen Ziffernfolgen, die irgendwo die Zahlenkette "007" enhalten. | ||
Eine rechtslineare Grammatik G der KGB-Sprache kann wie folgt definiert werden: | |||
* G= (N, T, S, P) | * G= (N, T, S, P) | ||
| Zeile 22: | Zeile 53: | ||
* '''Terminalsymbole''' T = {0,...,9} | * '''Terminalsymbole''' T = {0,...,9} | ||
* '''Startsymbol''' S = S | * '''Startsymbol''' S = S | ||
* '''Produktionsregeln P = { | * '''Produktionsregeln P = {''' | ||
** S → 0A | 1S | 2S | ... | 9S | ** S → 0A | 0S | 1S | 2S | ... | 9S | ||
** A → 0B | ** A → 0B | ||
** B → | ** B → 7C | ||
** C → ε | 0C | ... | 9C | ** C → ε | 0C | ... | 9C | ||
* '''}''' | |||
===Beispiel für die Ableitung eines Wortes=== | |||
Dass das Wort "060074" zu der KGB-Sprache gehört, lässt sich durch folgende Ableitung zeigen: | |||
* S → 0S → 06S → 060A → 0600B → 06007C → 060074C → 060074 | |||
Bei der letzten Ableitung wurde das C durch nichts (ε) ersetzt. | |||
===... und der Nachweis, dass sich ein Wort NICHT ableiten lässt=== | |||
Das kann viel schwieriger sein! | |||
Man muss nämlich <u>alle</u> Möglichkeiten durchprobieren und zeigen, dass <u>keine</u> zum Ziel führt! | |||
'''Nachweis, dass das Wort "0003" nicht zur KGB-Sprache gehört:''' | |||
* S → 0S → 00S → 000S → 0003S : Das Wort ist verbraucht, aber das Nicht-Terminal S ist nicht ersetzt. | |||
* S → 0S → 00S → 000A : Hier kann man mit dem Terminal 3 keine Ersetzungsregel anwenden. | |||
* S → 0S → 00A → 000B : Hier kann man mit dem Terminal 3 keine Ersetzungsregel anwenden. | |||
* S → 0A → 00B : Hier kann man mit dem Terminal 0 keine Ersetzungsregel anwenden. | |||
==Beispiel für eine nicht-reguläre Grammatik== | |||
Die folgende Grammatik für den KGB-Automaten ist <u>nicht</u> regulär: | |||
* G= (N, T, S, P) | |||
* '''Nichtterminalsymbole''' N = {S, A} | |||
* '''Terminalsymbole''' T = {0,...,9} | |||
* '''Startsymbol''' S = S | |||
* '''Produktionsregeln P = {''' | |||
** S → <u>007A</u> | 0S | 1S | 2S | ... | 9S | |||
** A → ε | 0A | ... | 9A | |||
* '''}''' | |||
Die unterstrichene Regel verstößt gegen die Anforderungen, denn vor dem Nicht-Terminalsymbol sind drei Terminalsymbole! | |||
''Hinweis:'' | |||
''Diese nicht-reguläre Grammatik lässt sich in eine reguläre Grammatik überführen.'' | |||
''Das gilt aber nicht für jede nicht-reguläre Grammatik!<br/>Z.B. die Grammatik mit der Produktionsregel <br/>S → aSb | ε<br/> lässt sich nicht in einen reguläre Grammatik überführen. <br/>Siehe [[Kontextfreie_Grammatik#Beispiel|Beispiel für eine kontextfreie Grammatik]]'' | |||
=Beziehung zu deterministischen endlichen Automaten= | |||
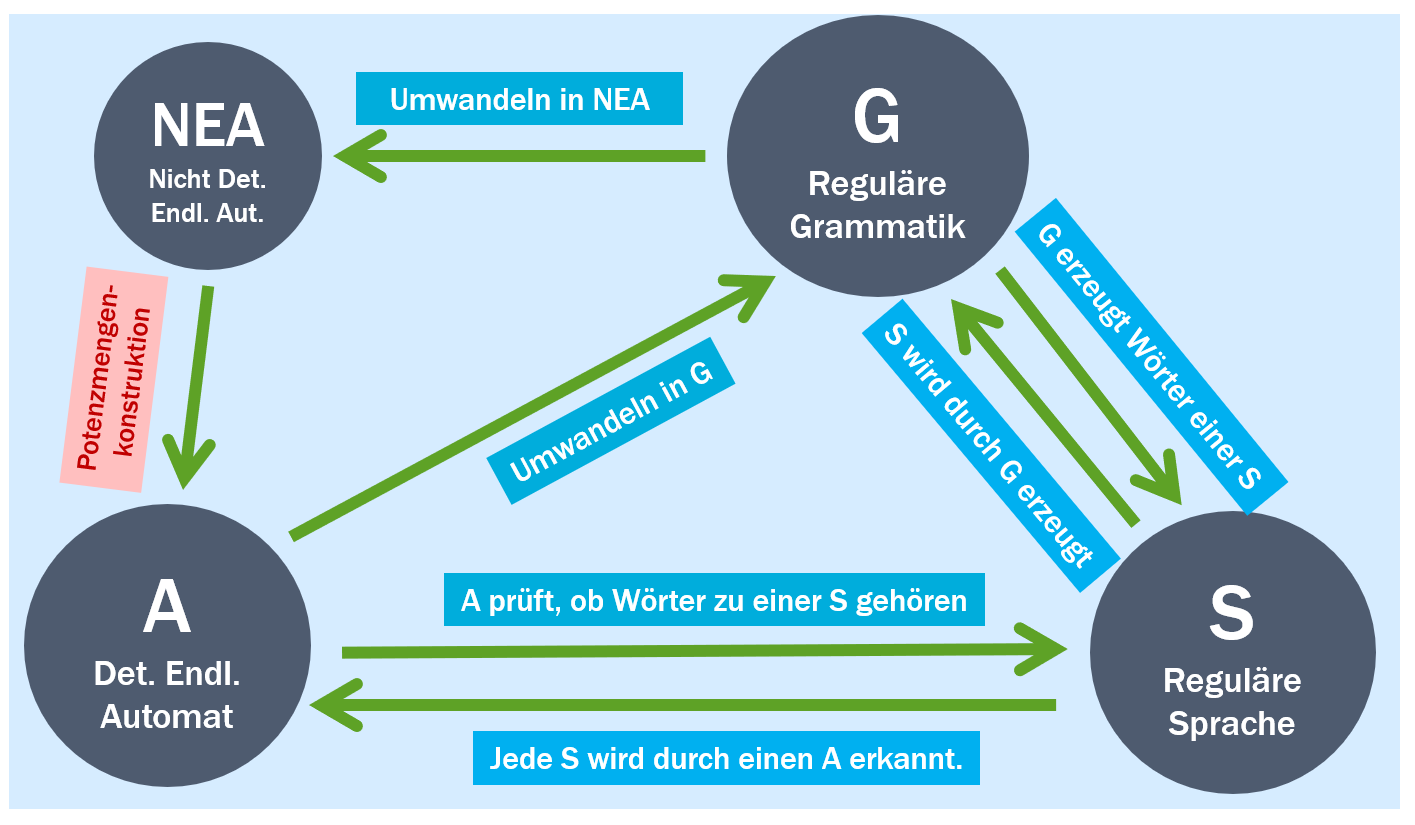
[[Datei:DEA-RG-NEA-reg-Sprache.png|400px|thumb|right|Beziehungen: Reguläre Grammatik - DEA - NEA - reguläre Sprache]] | |||
* '''Zu jeder [[reguläre Grammatik|regulären Grammatik]] gibt es einen deterministischen endlichen Automaten.'''<br> | |||
** Dazu erstellt man aus der regulären Grammatik erst einen [[Nicht-deterministischer endlicher Automaten|Nicht-deterministischen endlichen Automaten]], indem man aus jedem Nichtterminalsymbol einen Zustand macht und aus jeder Produktionsregel einen Übergang. | |||
** Aus dem [[Nicht-deterministischer endlicher Automaten|Nicht-deterministischen endlichen Automaten]] kann man einen deterministischen endlichen Automaten erstellen. Das ist mühsam, aber es ist bewiesen, dass das immer geht! | |||
* '''Zu jedem deterministischen endlichen Automaten gibt es eine [[reguläre Grammatik]].''' | |||
** Diese lässt sich leicht aus dem Übergangsgraphen konstruieren, indem man aus jedem Zustand ein Nichtterminalsymbol macht und aus jedem Übergang eine Regel (mit einem Terminalsymbol und einem Nichtterminalsymbol). | |||
** Erklärvideo dazu: [https://youtu.be/BcMXVx6VeSk Deterministischen endlichen Automaten in reguläre Grammatik umwandeln] | |||
=Beziehung zu regulären Sprachen= | |||
Aus der Beziehung zu den deterministischen endlichen Automaten folgt direkt: | |||
* '''Jede reguläre Grammatik erzeugt eine reguläre Sprache.''' | |||
** ''Denn zu jeder regulären Grammatik gibt es einen deterministischen endlichen Automaten, und dieser erkennt eine reguläre Sprache.'' | |||
* '''Zu jeder regulären Sprache gibt es eine reguläre Grammatik.''' | |||
** ''reguläre Sprachen sind genau die Sprachen, die von deterministischen endlichen Automaten erkannt werden. Zu jedem deterministischen endlichen Automaten kann man eine reguläre Grammatik finden.'' | |||
=Grenzen der regulären Grammatik= | |||
'''Für alle Sprachen, für die es keinen deterministischen endlichen Automaten gibt, gibt es auch keine reguläre Grammatik!''' | |||
Begründung: | |||
Wenn es für eine Sprache eine reguläre Grammatik gibt, dann kann man sie in einen deterministischen endlichen Automaten überführen. | |||
D.h. umgekehrt:<br/>Wenn es zu einer Sprache keinen deterministischen endlichen Automaten gibt, dann kann es zu der Sprache auch keine reguläre Grammatik geben. (Denn die ließe sich in einen deterministischen endlichen Automaten überführen.) | |||
==Beispiel== | |||
Für die Sprache L = {a<sup>n</sup>b<sup>n</sup>} gibt es keinen deterministischen endlichen Automaten:<br/>Siehe [[Deterministischer Endlicher Automat#Beispiel_2|Beispiel für Grenzen des deterministischen endlichen Automaten]]. | |||
Deswegen gibt es für diese Sprache auch keine reguläre Grammatik. | |||
Aktuelle Version vom 30. August 2023, 13:44 Uhr
Fachbegriffe
Nicht-terminal-symbole, Terminal-Symbole, Startsymbol, Produktionsregeln, Ableitung (eines Wortes), Sprache
Erklärvideos
Definition Grammatik
Eine Grammatik G wird durch ein 4-Tupel (N, T, S, P) definiert:
- N ist die Menge der Nichtterminalsymbole.
- T ist die Menge der Terminalsymbole.
- S ∈ N ist das Startsymbol.
- P ist die Menge der Produktionsregeln.
Reguläre Grammatik
Reguläre Grammatiken sind entweder rechtslinear oder linkslinear.
"Üblich" sind rechtslineare Grammatiken, weil sie sich aus DEAs und NEAs direkt herstellen lassen.
Linkslineare Grammatiken sind äquivalent zu rechtslinearen Grammatiken, d.h.:
- für jede linkslineare Grammatik gibt es eine rechtslineare Grammatik, die die gleiche Sprache erzeugt.
- für jede rechtslineare Grammatik gibt es eine linkslineare Grammatik, die die gleiche Sprache erzeugt.
rechtslineare Grammatik
Eine rechtslineare Grammatik ist eine Grammatik, bei der alle Produktionen eine der folgenden Formen haben:
- A → aB d.h. Nichtterminalsymbol wird ersetzt durch ein Terminalsymbol gefolgt von einem Nichtterminalsymbol. Das Nicht-Terminal steht rechts.
- A → a d.h. Nichtterminalsymbol wird ersetzt durch ein Terminalsymbol.
- A → ε d.h. Nichtterminalsymbol wird ersetzt durch nichts. (ε steht für nichts.)
linkslineare Grammatiken
in linkslinearen Grammatiken haben alle Regeln die Form:
- A → Ba d.h. Nichtterminalsymbol wird ersetzt durch ein Nichtterminalsymbol gefolgt von einem Terminalsymbol. Das Nicht-Terminal steht links.
- A → a d.h. Nichtterminalsymbol wird ersetzt durch ein Terminalsymbol.
- A → ε d.h. Nichtterminalsymbol wird ersetzt durch nichts. (ε steht für nichts.)
Das heißt: Der Unterschied zwischen regulären und linkslinearen Grammatiken besteht darin, dass bei den linkslinearen Grammatiken immer erst das Nichtterminalsymbol und dann das Terminalsymbol kommt.
Beispiele
KGB-Sprache
Die KGB-Sprache besteht aus allen Ziffernfolgen, die irgendwo die Zahlenkette "007" enhalten.
Eine rechtslineare Grammatik G der KGB-Sprache kann wie folgt definiert werden:
- G= (N, T, S, P)
- Nichtterminalsymbole N = {S, A, B, C}
- Terminalsymbole T = {0,...,9}
- Startsymbol S = S
- Produktionsregeln P = {
- S → 0A | 0S | 1S | 2S | ... | 9S
- A → 0B
- B → 7C
- C → ε | 0C | ... | 9C
- }
Beispiel für die Ableitung eines Wortes
Dass das Wort "060074" zu der KGB-Sprache gehört, lässt sich durch folgende Ableitung zeigen:
- S → 0S → 06S → 060A → 0600B → 06007C → 060074C → 060074
Bei der letzten Ableitung wurde das C durch nichts (ε) ersetzt.
... und der Nachweis, dass sich ein Wort NICHT ableiten lässt
Das kann viel schwieriger sein!
Man muss nämlich alle Möglichkeiten durchprobieren und zeigen, dass keine zum Ziel führt!
Nachweis, dass das Wort "0003" nicht zur KGB-Sprache gehört:
- S → 0S → 00S → 000S → 0003S : Das Wort ist verbraucht, aber das Nicht-Terminal S ist nicht ersetzt.
- S → 0S → 00S → 000A : Hier kann man mit dem Terminal 3 keine Ersetzungsregel anwenden.
- S → 0S → 00A → 000B : Hier kann man mit dem Terminal 3 keine Ersetzungsregel anwenden.
- S → 0A → 00B : Hier kann man mit dem Terminal 0 keine Ersetzungsregel anwenden.
Beispiel für eine nicht-reguläre Grammatik
Die folgende Grammatik für den KGB-Automaten ist nicht regulär:
- G= (N, T, S, P)
- Nichtterminalsymbole N = {S, A}
- Terminalsymbole T = {0,...,9}
- Startsymbol S = S
- Produktionsregeln P = {
- S → 007A | 0S | 1S | 2S | ... | 9S
- A → ε | 0A | ... | 9A
- }
Die unterstrichene Regel verstößt gegen die Anforderungen, denn vor dem Nicht-Terminalsymbol sind drei Terminalsymbole!
Hinweis:
Diese nicht-reguläre Grammatik lässt sich in eine reguläre Grammatik überführen.
Das gilt aber nicht für jede nicht-reguläre Grammatik!
Z.B. die Grammatik mit der Produktionsregel
S → aSb | ε
lässt sich nicht in einen reguläre Grammatik überführen.
Siehe Beispiel für eine kontextfreie Grammatik
Beziehung zu deterministischen endlichen Automaten
- Zu jeder regulären Grammatik gibt es einen deterministischen endlichen Automaten.
- Dazu erstellt man aus der regulären Grammatik erst einen Nicht-deterministischen endlichen Automaten, indem man aus jedem Nichtterminalsymbol einen Zustand macht und aus jeder Produktionsregel einen Übergang.
- Aus dem Nicht-deterministischen endlichen Automaten kann man einen deterministischen endlichen Automaten erstellen. Das ist mühsam, aber es ist bewiesen, dass das immer geht!
- Zu jedem deterministischen endlichen Automaten gibt es eine reguläre Grammatik.
- Diese lässt sich leicht aus dem Übergangsgraphen konstruieren, indem man aus jedem Zustand ein Nichtterminalsymbol macht und aus jedem Übergang eine Regel (mit einem Terminalsymbol und einem Nichtterminalsymbol).
- Erklärvideo dazu: Deterministischen endlichen Automaten in reguläre Grammatik umwandeln
Beziehung zu regulären Sprachen
Aus der Beziehung zu den deterministischen endlichen Automaten folgt direkt:
- Jede reguläre Grammatik erzeugt eine reguläre Sprache.
- Denn zu jeder regulären Grammatik gibt es einen deterministischen endlichen Automaten, und dieser erkennt eine reguläre Sprache.
- Zu jeder regulären Sprache gibt es eine reguläre Grammatik.
- reguläre Sprachen sind genau die Sprachen, die von deterministischen endlichen Automaten erkannt werden. Zu jedem deterministischen endlichen Automaten kann man eine reguläre Grammatik finden.
Grenzen der regulären Grammatik
Für alle Sprachen, für die es keinen deterministischen endlichen Automaten gibt, gibt es auch keine reguläre Grammatik!
Begründung:
Wenn es für eine Sprache eine reguläre Grammatik gibt, dann kann man sie in einen deterministischen endlichen Automaten überführen.
D.h. umgekehrt:
Wenn es zu einer Sprache keinen deterministischen endlichen Automaten gibt, dann kann es zu der Sprache auch keine reguläre Grammatik geben. (Denn die ließe sich in einen deterministischen endlichen Automaten überführen.)
Beispiel
Für die Sprache L = {anbn} gibt es keinen deterministischen endlichen Automaten:
Siehe Beispiel für Grenzen des deterministischen endlichen Automaten.
Deswegen gibt es für diese Sprache auch keine reguläre Grammatik.