Potenzmengenkonstruktion
Schon die Überschrift verspricht eine komplizierte, mühsame und langwierige Prozedur - und so ist es leider auch.
Aber das Zentralabitur will die Informatik-Schüler in NRW trotzdem damit beglücken...
Wozu?
Mithilfe der Potenzmengenkonstruktion kann man einen Deterministischen Endlicher Automat (DEA)in einen Nicht-deterministischen endlichen Automaten (NEA) überführen.
Grundidee
Die Grundidee ist reichlich abstrakt und hier - mit Absicht - sehr kurz gehalten. Man kann das sowieso erst verstehen, wenn man mal ein Beispiel durchexerziert hat...
Der NEA kann sich bei gleicher Zeichenfolge "zeitgleich" in mehreren verschiedenen Zuständen befinden - je nachdem, welchen "Weg" man bei einem nicht-deterministischen Übergang gewählt hat.
Ein Zustand des DEA fasst all diejenigen Zustände des NEA zusammen, in denen sich der NEA zu einem bestimmten Zeitpunkt befinden könnte.
Beispiel
Youtube-Tutorial
Wer Youtube-Erklärungen mag, ist hier richtig: NEA zu DEA Transformation (Youtube).
Man muss aber mindestens 17 Minuten Zeit haben, um die beiden Teile des Tutorials anzusehen! Und um es richtig zu verstehen, muss man vermutlich ab und zu nochmal zurückspulen...
Konventionell
Das folgende Beispiel kommt von Potenzmengenkonstruktion Wikipedia und ist dort unter der CC BY-SA 3.0 veröffentlicht.
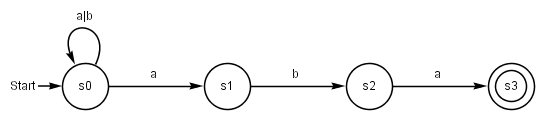
Ausgangspunkt
Übergangsfunktion des NEA
Der NEA lässt sich mithilfe einer Übergangsfunktion so beschreiben:
- [math]\displaystyle{ \mathcal{NEA} = (Q, A, \delta, S, E ) }[/math]
- Alphabet: [math]\displaystyle{ A\!\, = \{a, b\} }[/math]
- Menge der Zustände: [math]\displaystyle{ Q = \{s_0, s_1, s_2, s_3\} }[/math]
- Startzustand: [math]\displaystyle{ S = s_0 }[/math]
- Menge der Endzustände: [math]\displaystyle{ E = \{s_3\} }[/math]
- tabellarische Übertragungsfunktion [math]\displaystyle{ \delta\!\, }[/math]:
| NEA | a | b |
|---|---|---|
| [math]\displaystyle{ s_0\!\, }[/math] | [math]\displaystyle{ \{s_0\!\,, s_1\} }[/math] | [math]\displaystyle{ \{s_0\}\!\, }[/math] |
| [math]\displaystyle{ s_1\!\, }[/math] | [math]\displaystyle{ \emptyset }[/math] | [math]\displaystyle{ \{s_2\}\!\, }[/math] |
| [math]\displaystyle{ s_2\!\, }[/math] | [math]\displaystyle{ \{s_3\}\!\, }[/math] | [math]\displaystyle{ \emptyset }[/math] |
| [math]\displaystyle{ s_3\!\, }[/math] | [math]\displaystyle{ \emptyset }[/math] | [math]\displaystyle{ \emptyset }[/math] |
Hinweis: [math]\displaystyle{ \emptyset }[/math] ist die leere Menge. Man sieht also:
Mit jedem Übergang kann man mehrere Zustände erreichen; diese werden als Menge von Zuständen angegeben.
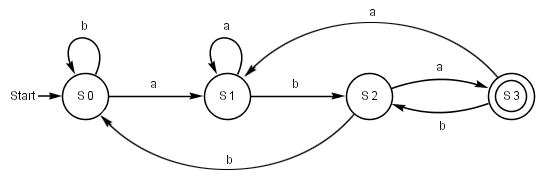
Konstruktion des zugehörigen DEA
Die Zustandsmenge [math]\displaystyle{ Q\!\,' = \{S_0', S_1', S_2', S_3'\} }[/math] und die Übertragungsfunktion [math]\displaystyle{ \delta\!\,' }[/math] des äquivalenten DEA ergibt sich wie folgt:
| δ' | a | b |
|---|---|---|
| [math]\displaystyle{ S_0\!\,' = \{s_0\} }[/math] | [math]\displaystyle{ \{s_0, s_1\}\!\, }[/math] | [math]\displaystyle{ \{s_0\}\!\, }[/math] |
| [math]\displaystyle{ S_1\!\,' = \{s_0, s_1\} }[/math] | [math]\displaystyle{ \{s_0, s_1\}\!\, }[/math] | [math]\displaystyle{ \{s_0, s_2\}\!\, }[/math] |
| [math]\displaystyle{ S_2\!\,' = \{s_0, s_2\} }[/math] | [math]\displaystyle{ \{s_0, s_1, s_3\}\!\, }[/math] | [math]\displaystyle{ \{s_0\}\!\, }[/math] |
| [math]\displaystyle{ S_3\!\,' = \{s_0, s_1, s_3\} }[/math] | [math]\displaystyle{ \{s_0, s_1\}\!\, }[/math] | [math]\displaystyle{ \{s_0, s_2\}\!\, }[/math] |
Damit ein Zustand des DEA ein Endzustand ist, muss er mindestens einen Endzustand des NEA enthalten. (Denn im NEA reicht es für das Erkennen eines Wortes, wenn es "mindestens einen Weg gibt".
Endzustände des DEA
Im Beispiel ergibt sich als Menge der Endzustände [math]\displaystyle{ E\!\,' = \{S_3'\} }[/math] , da nur [math]\displaystyle{ S_3\!\,' = \{s_0, s_1, s_3\} }[/math] den Endzustand [math]\displaystyle{ s_3\!\, }[/math] des NEA enthält. Insgesamt ergibt sich der deterministische Automat [math]\displaystyle{ \mathcal{A} = (Q', \Sigma, \delta', s_0', E') }[/math], der folgende graphische Darstellung besitzt: