Nicht-deterministischer endlicher Automaten

Nichtdeterministische endliche Automaten unterscheiden sich von Deterministischen endlichen Automaten nur in einem wesentlichen Punkt:

• Die Übergänge zwischen den Zuständen sind nicht eindeutig.

D.h. es kann für ein Symbol und einen Zustand mehrere mögliche Übergänge geben.

Ein Wort gilt als akzeptiert, wenn es für das Wort einen Übergang vom Anfangs- in einen Endzustand gibt.

Beispiel

Der KGB-Automat als Nicht-deterministischer endlicher Automat.

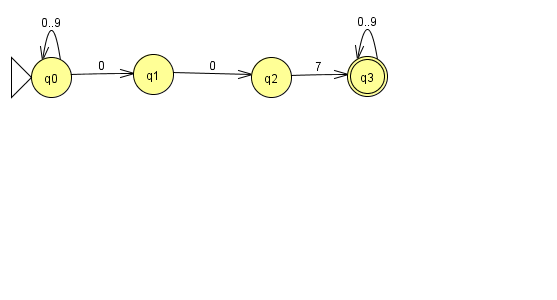
Der KGB-Automat erkennt Wörter, die nur aus den Ziffern 0,...,9 bestehen und die irgendwo die Zahlenkette "007" enhalten.

Man sieht, dass im Zustand q0 der Übergang für die 0 nicht eindeutig ist; man kann entweder bei q₀ bleiben oder zu q₁ übergehen.

Die Darstellung als Nicht-deterministischer endlicher Automat ist oft viel einfacher als die Darstellung als Deterministischer Endlicher Automat.

Beziehung zu deterministischen endlichen Automaten

• Jeder deterministische endliche Automat ist (ohne irgendwelches Dazutun) direkt auch ein Nicht-deterministischer endlicher Automat.
• Zu jedem Nicht-deterministischen endlichen Automaten kann man eine deterministischen endlichen Automaten konstruieren. Das Verfahren dazu heißt Potenzmengenkonstruktion und ist reichlich kompliziert, funktioniert aber immer! (Das ist mathematisch bewiesen...)

Beziehung zu regulären Grammatiken

• Zu jeder regulären Grammatik lässt sich einfach ein nicht-deterministischer endlicher Automat konstruieren:
  • Aus jedem Nichtterminalsymbol wird einen Zustand des Automaten gemacht und aus jeder Produktionsregel einen Übergang des Automaten.
• Der Nicht-deterministische endliche Automat ist deswegen ein Zwischenschritt beim Übergang von der regulären Grammatik zum deterministischen endlichen Automaten.