Deterministischer Endlicher Automat: Unterschied zwischen den Versionen
| (6 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 14: | Zeile 14: | ||
Deterministische endliche Automaten können als Java-Programm realisiert werden. Ein solches Programm nennt man '''[[Parser]]'''. | Deterministische endliche Automaten können als Java-Programm realisiert werden. Ein solches Programm nennt man '''[[Parser]]'''. | ||
=Fachbegriffe= | |||
Deterministischer endlicher Automat (DEA), Zustand, Anfangszustand, Endzustände, Alphabet, Übergang, Zustandsübergangsfunktion, Übergangsgraph, prüfen | |||
=Erklärvideos= | |||
* [https://youtu.be/BcMXVx6VeSk Deterministischen endlichen Automaten in reguläre Grammatik umwandeln] | |||
=Beispiel= | =Beispiel= | ||
| Zeile 51: | Zeile 57: | ||
'''Beispiele:''' | '''Beispiele:''' | ||
* Überprüfung von "060074": | * Überprüfung von "060074": | ||
<code> | <code> 0 6 0 0 7 4 | ||
q<sub>0</sub> → q<sub>1</sub> → q<sub>0</sub> → q<sub>1</sub> → q<sub>2</sub> → q<sub>3</sub> → q<sub>3</sub> | q<sub>0</sub> → q<sub>1</sub> → q<sub>0</sub> → q<sub>1</sub> → q<sub>2</sub> → q<sub>3</sub> → q<sub>3</sub> | ||
Endzustand erreicht, d.h. akzeptiert. | Endzustand erreicht, d.h. akzeptiert.</code> | ||
</code> | * Überprüfung von "060064": | ||
* Überprüfung von "060064": q<sub>0</sub> → q<sub>1</sub> →q<sub>0</sub> →q<sub>1</sub> →q<sub>2</sub> →q<sub>0</sub> →q<sub>0</sub> : Endzustand <u>nicht</u> erreicht, d.h. <u>nicht</u> akzeptiert. | <code> 0 6 0 0 6 4 | ||
q<sub>0</sub> → q<sub>1</sub> → q<sub>0</sub> → q<sub>1</sub> → q<sub>2</sub> → q<sub>0</sub> → q<sub>0</sub> : | |||
Endzustand <u>nicht</u> erreicht, d.h. <u>nicht</u> akzeptiert. | |||
</code> | |||
''In diesem Beispiel kann nicht demonstriert werden, wie man in eine Senke fahren kann, weil es es in jedem Zustand für jedes Symbol einen Übergang gibt.'' | ''In diesem Beispiel kann nicht demonstriert werden, wie man in eine Senke fahren kann, weil es es in jedem Zustand für jedes Symbol einen Übergang gibt.'' | ||
| Zeile 71: | Zeile 79: | ||
=Beziehung zu regulären Sprachen und regulären Grammatiken= | =Beziehung zu regulären Sprachen und regulären Grammatiken= | ||
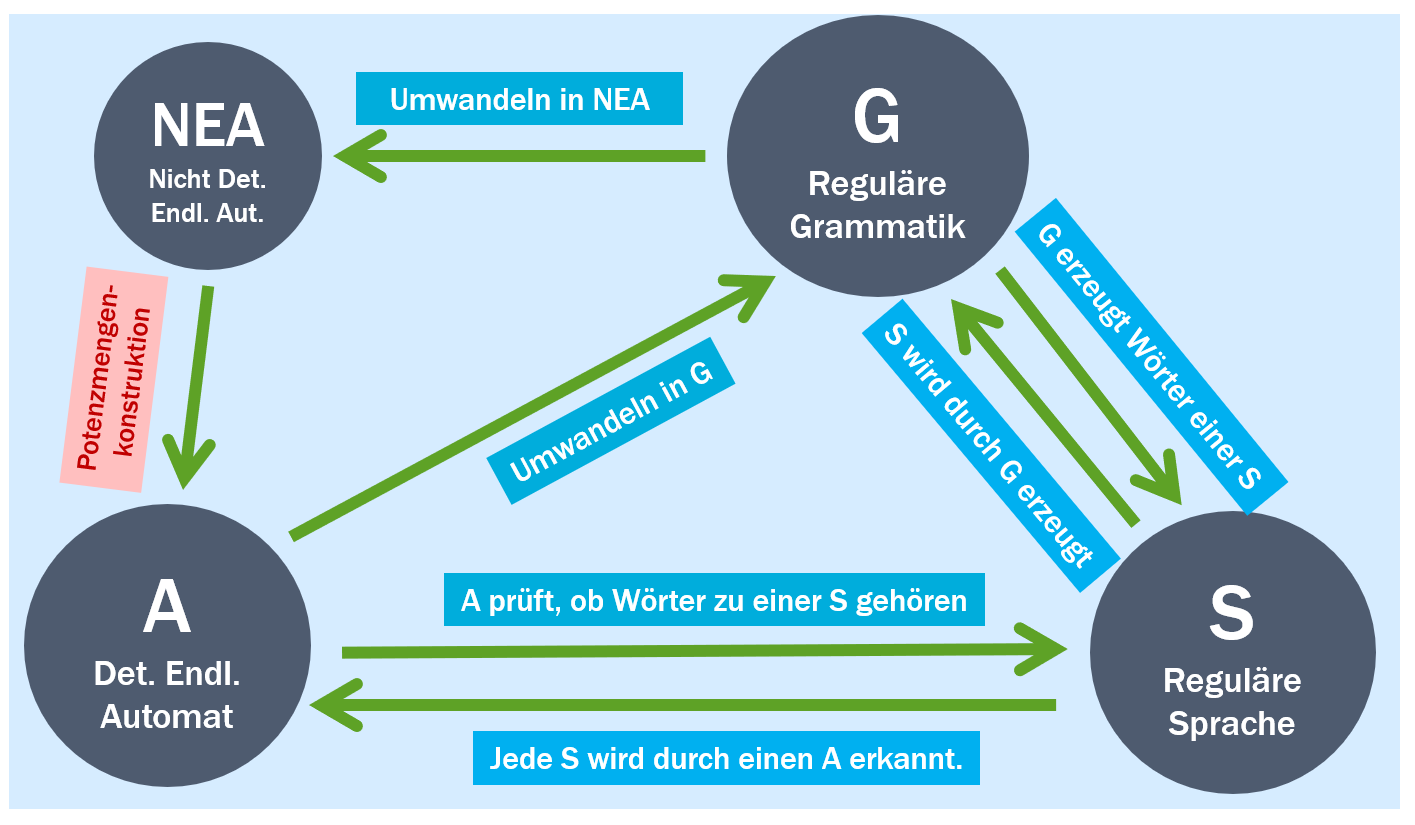
[[Datei:DEA-RG-NEA-reg-Sprache.png|400px|thumb|right|Beziehungen: Reguläre Grammatik - DEA - NEA - reguläre Sprache]] | |||
* Sprachen, die von deterministischen endlichen Automaten akzeptiert werden, heißen '''reguläre Sprache'''. | * Sprachen, die von deterministischen endlichen Automaten akzeptiert werden, heißen '''reguläre Sprache'''. | ||
* '''Zu jedem deterministischen endlichen Automaten gibt es eine [[reguläre Grammatik]].''' | * '''Zu jedem deterministischen endlichen Automaten gibt es eine [[reguläre Grammatik]].''' | ||
** Diese lässt sich leicht aus dem Übergangsgraphen konstruieren, indem man aus jedem Zustand ein Nichtterminalsymbol macht und aus jedem Übergang eine Regel (mit einem Terminalsymbol und einem Nichtterminalsymbol). | ** Diese lässt sich leicht aus dem Übergangsgraphen konstruieren, indem man aus jedem Zustand ein Nichtterminalsymbol macht und aus jedem Übergang eine Regel (mit einem Terminalsymbol und einem Nichtterminalsymbol). | ||
** Erklärvideo dazu: [https://youtu.be/BcMXVx6VeSk Deterministischen endlichen Automaten in reguläre Grammatik umwandeln] | |||
* '''Zu jeder [[reguläre Grammatik|regulären Grammatik]] gibt es einen deterministischen endlichen Automaten.'''<br> | * '''Zu jeder [[reguläre Grammatik|regulären Grammatik]] gibt es einen deterministischen endlichen Automaten.'''<br> | ||
** Dazu erstellt man aus der regulären Grammatik erst einen [[Nicht-deterministischer endlicher Automaten|Nicht-deterministischen endlichen Automaten]], indem man aus jedem Nichtterminalsymbol einen Zustand macht und aus jeder Produktionsregel einen Übergang. | ** Dazu erstellt man aus der regulären Grammatik erst einen [[Nicht-deterministischer endlicher Automaten|Nicht-deterministischen endlichen Automaten]], indem man aus jedem Nichtterminalsymbol einen Zustand macht und aus jeder Produktionsregel einen Übergang. | ||
| Zeile 93: | Zeile 103: | ||
'''Begründung:''' Der Automat muss sich "merken" können, wie viele a vorgekommen sind. Dafür bräuchte er eine unbegrenzte Menge von Zuständen, denn es ist nicht festgelegt, wie viele Buchstaben "a" kommen, bevor man zu "b" übergeht. | '''Begründung:''' Der Automat muss sich "merken" können, wie viele a vorgekommen sind. Dafür bräuchte er eine unbegrenzte Menge von Zuständen, denn es ist nicht festgelegt, wie viele Buchstaben "a" kommen, bevor man zu "b" übergeht. | ||
'''Hinweis:'''<br> | |||
Für die Sprache <code>a<sup>n</sup>b<sup>n</sup></code> kann man einen '''[[Kellerautomat]]''' entwickeln. | |||
==Weitere Beispiele== | ==Weitere Beispiele== | ||
Aktuelle Version vom 30. August 2023, 13:43 Uhr
Ein deterministischer endlicher Automat erhält ein Wort als Eingabe und akzeptiert dieses Wort oder nicht.
Die Menge der akzeptierten Wörter bildet die durch den deterministischen endlichen Automaten dargestellte Sprache.
Sprachen, die von deterministischen endlichen Automaten akzeptiert werden, heißen reguläre Sprache.
Zu unterscheiden ist der deterministische endliche Automat vom Nicht-deterministischen endlichen Automaten.
Deterministische endliche Automaten können als Java-Programm realisiert werden. Ein solches Programm nennt man Parser.
Fachbegriffe
Deterministischer endlicher Automat (DEA), Zustand, Anfangszustand, Endzustände, Alphabet, Übergang, Zustandsübergangsfunktion, Übergangsgraph, prüfen
Erklärvideos
Beispiel
Der KGB-Automat:
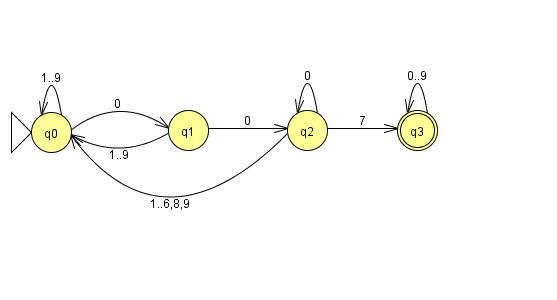
Der KGB-Automat erkennt Wörter, die nur aus den Ziffern 0,...,9 bestehen und die irgendwo die Zahlenkette "007" enhalten.
- Eingabealphabet: A = {0, 1, ..., 9}
- Zustände: Z = {q0, q1, q2, q3}
- Die Zustandsübergangsfunktion wird durch den Übergangsgraph (rechts) oder die Übergangstabelle (unten) dargestellt.
- Anfangszustand: q0 (im Graph: ein Dreieck)
- Endzustände: {q3} (im Graph: ein Doppelkreis)
Die Zustandsübergangsfunktion als Tabelle dargestellt:
| 0 | 7 | 1..6, 8, 9 | |
|---|---|---|---|
| q0 | q1 | q0 | q0 |
| q1 | q2 | q0 | q0 |
| q2 | q2 | q3 | q0 |
| q3 | q3 | q3 | q3 |
Überprüfung von Wörtern
Bei der Überprüfung von Wörtern mit deterministischen endlichen Automaten gibt es drei Möglichkeiten:
- Es wird ein Endzustand erreicht: Dann ist das Wort akzeptiert.
- Es wird kein Endzustand erreicht: Dann ist das Wort nicht akzeptiert.
- Es gibt für ein Zeichen im Wort von dem Zustand aus, der gerade erreicht ist, keinen Übergang: Dann "fährt" man in eine sog. Senke und das Wort ist nicht akzeptiert.
Beispiele:
- Überprüfung von "060074":
0 6 0 0 7 4
q0 → q1 → q0 → q1 → q2 → q3 → q3
Endzustand erreicht, d.h. akzeptiert.
- Überprüfung von "060064":
0 6 0 0 6 4
q0 → q1 → q0 → q1 → q2 → q0 → q0 :
Endzustand nicht erreicht, d.h. nicht akzeptiert.
In diesem Beispiel kann nicht demonstriert werden, wie man in eine Senke fahren kann, weil es es in jedem Zustand für jedes Symbol einen Übergang gibt.
Definition
Ein deterministischer, endlicher Automat wird durch ein 5-Tupel (A, Z, d, q0, E) spezifiziert:
- Das Eingabealphabet A ist eine endliche, nicht leere Menge von Symbolen. Buchstaben des Eingabealphabetes werden in der Regel klein geschrieben.
- Z ist eine endliche, nicht leere Menge von Zuständen Z
- d: Z x A → Z ist die Zustandsübergangsfunktion
- q0 ∈ Z ist der Anfangszustand
- E ⊆ Z ist die Menge der Endzustände
Die Zustandsübergangsfunktion kann durch einen Übergangsgraphen oder durch eine Tabelle dargestellt werden.
Beziehung zu regulären Sprachen und regulären Grammatiken
- Sprachen, die von deterministischen endlichen Automaten akzeptiert werden, heißen reguläre Sprache.
- Zu jedem deterministischen endlichen Automaten gibt es eine reguläre Grammatik.
- Diese lässt sich leicht aus dem Übergangsgraphen konstruieren, indem man aus jedem Zustand ein Nichtterminalsymbol macht und aus jedem Übergang eine Regel (mit einem Terminalsymbol und einem Nichtterminalsymbol).
- Erklärvideo dazu: Deterministischen endlichen Automaten in reguläre Grammatik umwandeln
- Zu jeder regulären Grammatik gibt es einen deterministischen endlichen Automaten.
- Dazu erstellt man aus der regulären Grammatik erst einen Nicht-deterministischen endlichen Automaten, indem man aus jedem Nichtterminalsymbol einen Zustand macht und aus jeder Produktionsregel einen Übergang.
- Aus dem Nicht-deterministischen endlichen Automaten kann man einen deterministischen endlichen Automaten erstellen. Das ist mühsam, aber es ist bewiesen, dass das immer geht!
Grenzen
Nicht jede Sprache kann durch einen deterministischen endlichen Automaten erkannt werden.
Die wesentliche Grenze ist hierbei, dass der Automat endlich sein muss.
Beispiel
Gegeben ist eine Sprache, die aus dem Alphabet A = {a, b} besteht.
Zur Sprache sollen die Wörter der Form anbn gehören, d.h. alle Wörter für die gilt:
- erst beliebig viele a
- dann genauso viele b.
Für diese Sprache gibt es keinen deterministischen endlichen Automaten!
Begründung: Der Automat muss sich "merken" können, wie viele a vorgekommen sind. Dafür bräuchte er eine unbegrenzte Menge von Zuständen, denn es ist nicht festgelegt, wie viele Buchstaben "a" kommen, bevor man zu "b" übergeht.
Hinweis:
Für die Sprache anbn kann man einen Kellerautomat entwickeln.
Weitere Beispiele
Auch für die folgenden Sprachen gibt es keinen deterministischen endlichen Automaten.
- Die spiegelsymmetrische Sprache: Jedes Wort soll in der Mitte eine Spiegelachse haben, d.h. die erste Worthälfte soll spiegelsymmetrisch zur zweiten Worthälfte sein.
- Die Sprache der Doppelwörter: Zu dieser Sprache gehören genau die Wörter, die aus zwei gleichen Wörtern bestehen.